��Ŀ����
���и��¼�����������ij��˾����480��Ԫ����ij�ֲ�Ʒ��������������һ��Ͷ���ʽ�1520��Ԫ���������豸�����иò�Ʒ�������ӹ�����֪�������ֲ�Ʒÿ������ɱ���40Ԫ�������г����з��֣��ò�Ʒ�����۵��ۣ��趨��100Ԫ��300Ԫ֮���Ϊ�����������۵��۶�Ϊ100Ԫʱ����������Ϊ20����������۵��۳���100Ԫ����������200Ԫʱ��ÿ���²�Ʒ�����ۼ۸�ÿ����10Ԫ����������������0.8����������۵��۳���200Ԫ����������300Ԫʱ��ÿ����Ʒ�����ۼ۸�ÿ����10Ԫ����������������1����������۵���Ϊx��Ԫ������������Ϊy��������������Ϊw����Ԫ�����������=�����۶�-�����ɱ�-Ͷ�ʳɱ���
��1��ֱ��д��y��x֮��ĺ�����ϵʽ��
��2�����һ��������w��x��ĺ�����ϵʽ����˵��Ͷ�ʵĵ�һ�꣬�ù�˾��ӯ�����ǿ�����ӯ������������Ƕ��٣����������ٿ����Ƕ��٣�
��3�����ù�˾ϣ�����ڶ���ף���ȥ��һ������ӯ��������С���𣩺��������ӯ��������1842Ԫ������ȷ����ʱ���۵��۵ķ�Χ���ڴ�����£�Ҫʹ��Ʒ������������۵���Ӧ��Ϊ����Ԫ��
(1)y=-0.08x+28, 100��x��200;y=-0.1x+32��200��x��300��(2) ��һ����100��x��200ע������x=195ʱ�������٣�Ϊ78��Ԫ; (3)190Ԫ.
���������������1�����������г�����xy�ķ��̼��ɣ�
��2������������������κ�������ʽ�������ҳ���ֵ�Լ���Ӧ���Ա�����Χ��
��3��������������ۣ��ҳ���ֵ�Լ���Ӧ���Ա���ȡֵ��Χ��
�������������1�������Ȼ��һ���ֶκ�����
y=20- =-0.08x+28
=-0.08x+28
100��x��200��
�ɼ�x=200Ԫʱ��y=28-16=12���������
y=12- =-0.1x+32��200��x��300��
=-0.1x+32��200��x��300��
��2��Ͷ�ʳɱ�Ϊ480+1520=2000��Ԫ
y=-0.08x+28��100��x��200��
w=xy-40y-2000
=��x-40����-0.08x+28��-2000
=-0.08x2+31.2x-3120
=-0.08��x-195��2-78
�ɼ���һ����100��x��200ע������x=195ʱ�������٣�Ϊ78��Ԫ
��3���������ӯ��������1842��Ԫ���ɼ��ڶ�������Ҫӯ��1842+78=1920��Ԫ����Ȼ����һ���㣬�ڶ������ǾͲ�����Ͷ�ʳɱ���2000��Ԫ�ˣ�
�ڶ��꣺100��x��200ʱ��ӯ����xy-40y=-0.08��x-195��2+1922��1920
�ⲻ��ʽ�õ���190��x��200
��ʱ���ٿ�y=-0.08x+28���ɼ�x=190ʱ��y���=12.8
���Զ���190Ԫʱ�����������
���㣺���κ�����Ӧ�ã�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д� �ϵ����㣬��y1��y2�Ĵ�С��ϵΪy1 y2���>����<����������
�ϵ����㣬��y1��y2�Ĵ�С��ϵΪy1 y2���>����<����������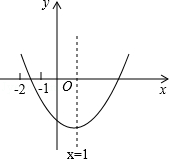
 �ĸ���
�ĸ��� ��
�� ��
�� ����CD=3��
����CD=3�� ��ͼ���ϣ���k=��1��
��ͼ���ϣ���k=��1��
 �У����κ���
�У����κ��� ��ͼ����
��ͼ���� �ύ�ڵ�A��B����B�ڵ�A����ࣩ����
�ύ�ڵ�A��B����B�ڵ�A����ࣩ���� �ύ�ڵ�C��������H��0,
�ύ�ڵ�C��������H��0,  ����ƽ����
����ƽ���� ����DEΪֱ������Q������Q��
����DEΪֱ������Q������Q��

