题目内容
计算(1)计算|-
| 1 |
| 2 |
| 9 |
(2)解方程(
| x |
| x+1 |
| x |
| x+1 |
分析:(1)此题涉及到绝对值,开方,0次幂,特殊角的三角函数值四个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果;
(2)设
=y,原方程变为y2-y-2=0,解一元二次方程可得到
的值,再求出x的值即可得答案.
(2)设
| x |
| x+1 |
| x |
| x+1 |
解答:(1)解:原式=
-3+1-
=-2;
(2)解:设
=y,则原方程可化为y2-y-2=0.
解得y1=2,y2=-1,
当
=2,解得x=-2;
当
=-1,解得x=-
.
经检验x1=-2,x2=-
都是原方程的根.
| 1 |
| 2 |
| 1 |
| 2 |
(2)解:设
| x |
| x+1 |
解得y1=2,y2=-1,
当
| x |
| x+1 |
当
| x |
| x+1 |
| 1 |
| 2 |
经检验x1=-2,x2=-
| 1 |
| 2 |
点评:此题主要考查了实数的综合运算能力和换元法解分式方程,解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算,解分式方程不要忘记检验.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
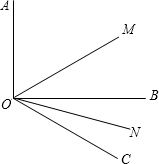 (1)如图所示,∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数.
(1)如图所示,∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数.