Question

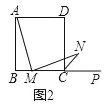
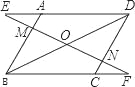
【题目】已知：如图在平行四边形ABCD中，过对角线BD的中点O作直线EF分别交DA的延长线、AB、DC、BC的延长线于点E、M、N、F．

（1）观察图形并找出一对全等三角形：△_≌△_，请加以证明；

（2）在（1）中你所找出的一对全等三角形，其中一个三角形可由另一个三角形经过怎样的变换得到？

Answer 1

【答案】（1）△DOE≌△BOF；证明见解析；（2）绕点O旋转180°后得到或以点O为中心作对称变换得到．

【解析】

（1）本题要证明如△ODE≌△BOF，已知四边形ABCD是平行四边形，具备了同位角、内错角相等，又因为OD=OB，可根据AAS能判定△DOE≌△BOF；

（2）平行四边形是中心对称图形，这对全等三角形中的一个是以其中另一个三角形绕点O旋转180°后得到或以点O为中心作对称变换得到．

（1）△DOE≌△BOF；

证明：∵四边形ABCD是平行四边形，

∴AD∥BC．

∴∠EDO=∠FBO，∠E=∠F．

又∵OD=OB，

∴△DOE≌△BOF（AAS）．

（2）绕点O旋转180°后得到或以点O为中心作对称变换得到．