题目内容
【题目】已知抛物线y= ![]() x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为(
x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为( ![]() ,3),P是抛物线y=
,3),P是抛物线y= ![]() x2+1上一个动点,则△PMF周长的最小值是( )
x2+1上一个动点,则△PMF周长的最小值是( ) 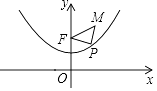
A.3
B.4
C.5
D.6
【答案】C
【解析】解:过点M作ME⊥x轴于点E,交抛物线y= ![]() x2+1于点P,此时△PMF周长最小值, ∵F(0,2)、M(
x2+1于点P,此时△PMF周长最小值, ∵F(0,2)、M( ![]() ,3),
,3),
∴ME=3,FM= ![]() =2,
=2,
∴△PMF周长的最小值=ME+FM=3+2=5.
故选C.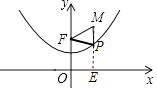
【考点精析】关于本题考查的二次函数的性质和三角形三边关系,需要了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;三角形两边之和大于第三边;三角形两边之差小于第三边;不符合定理的三条线段,不能组成三角形的三边才能得出正确答案.

练习册系列答案
相关题目