题目内容
如图,正三角形ABC的边长为1,E、F、G分别是AB、BC、CA上的点,且AE=BF=CG,设△EFG的面积为y,AE的长为x,则y关于x的函数的图象大致是( ▲ )

C
分析:根据题意,易得△AEG、△BEF、△CFG三个三角形全等,且在△AEG中,AE=x,AG=1-x;可得△AEG的面积y与x的关系;进而可判断得则y关于x的函数的图象的大致形状.
解:根据题意,有AE=BF=CG,且正三角形ABC的边长为1,
故BE=CF=AG=1-x;
故△AEG、△BEF、△CFG三个三角形全等.
在△AEG中,AE=x,AG=1-x,
则S△AEG=
 AE×AG×sinA=
AE×AG×sinA= x(1-x);
x(1-x);故y=S△ABC-3S△AEG=
 -3×
-3× x(1-x)=
x(1-x)= (3x2-3x+1).
(3x2-3x+1).故可得其图象为二次函数,且开口向上;
故选C.

练习册系列答案
相关题目
 ,下列结论正确的是………………( )
,下列结论正确的是………………( ) 的左侧部分函数的图像是上升的;
的左侧部分函数的图像是上升的;  的左侧部分函数的图像是上升的;
的左侧部分函数的图像是上升的;  ,令
,令 ,可得
,可得 ,我们就说
,我们就说 是函数
是函数 (k为常数).当k=2时,求该函数的零点;
(k为常数).当k=2时,求该函数的零点;
 ,△ABC与正方
,△ABC与正方 ,则
,则
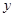 (元/千克)与月份
(元/千克)与月份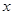 之间满足一次函数关系
之间满足一次函数关系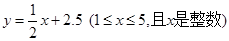 。其月销售量
。其月销售量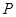 (千克)与月份
(千克)与月份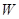 (元)最大?最大金额是多少元?
(元)最大?最大金额是多少元?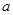 %,当销售了这批果冻的四分之三后,考虑到制作和营运成本的提高,生产商将批发价提高了
%,当销售了这批果冻的四分之三后,考虑到制作和营运成本的提高,生产商将批发价提高了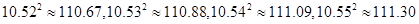 )
)