题目内容
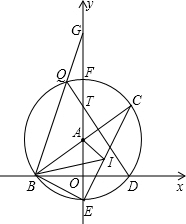
如图,直线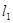 交直线
交直线 于
于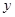 轴上一点
轴上一点 ,交
,交 轴上另一点
轴上另一点 ,
, 交
交 轴于另一点
轴于另一点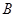 ,二次函数
,二次函数 (
(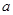 >0)的图像过点
>0)的图像过点 、
、 两点,点
两点,点 是线段
是线段 上由
上由 向
向 移动的动点,线段
移动的动点,线段 (1<
(1< <8)。
<8)。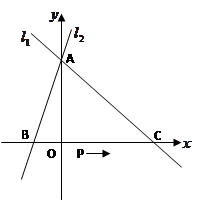
⑴
 为何值时,
为何值时, 为圆心
为圆心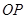 为半径的圆与
为半径的圆与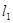 相切;
相切;⑵设抛物线对称轴与直线
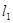 相交于点
相交于点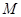 ,请在
,请在 轴上求一点
轴上求一点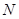 ,使
,使 的周长最小;
的周长最小;⑶设点
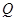 是
是 上由
上由 向
向 移动的一动点,且
移动的一动点,且 ,若
,若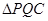 的面积为
的面积为 ,求
,求 与
与 的函数关系式,当
的函数关系式,当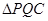 为等腰三角形时,请直接写出
为等腰三角形时,请直接写出 的值。
的值。
⑴3⑵( ⑶
⑶ ,①PQ=PC 则t=
,①PQ=PC 则t= ,②CP=CQ 则 t=4,
,②CP=CQ 则 t=4,
③QC=QP 则 t=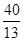 解析:
解析:
解:⑴∵B、C在x轴上且抛物线经过B、C两点
∴令 且
且 >0
>0
∴ 即B(-2,0)、C(8,0)
即B(-2,0)、C(8,0)
在Rt , OA=6,OC=8, ∴AC=10
, OA=6,OC=8, ∴AC=10
过点P作PE⊥AC,垂足为E,则易证 ∽
∽
∴ ∴
∴ ∴
∴
当P为圆心,OP 为半径的圆与 相切时,即PE=OP
相切时,即PE=OP
∴ 则
则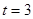 (3分)
(3分)
⑵抛物线的对称轴为
直线 经过A(0,6)、C(8,0), 易求
经过A(0,6)、C(8,0), 易求 的解析式为
的解析式为 ∴M(3,
∴M(3,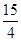 )
)
为求得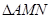 的周长最小,作点A 的关于x轴的对称点
的周长最小,作点A 的关于x轴的对称点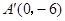
则经过 、M两点的直线与x轴的交点即为点N
、M两点的直线与x轴的交点即为点N
∴直线 M的解析式为
M的解析式为 ∴N(
∴N( (6分)
(6分)
⑶ 与
与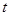 的函数关系式为
的函数关系式为
若 为等腰三角形,分三种情况:
为等腰三角形,分三种情况:
①PQ=PC 则t=
②CP=CQ 则 t=4
③QC=QP 则 t=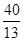 (9分)
(9分)
⑴由已知求得B、C两点的坐标,过点P作PE⊥AC,垂足为E,证得 ∽
∽ ,得出PE的长,求出
,得出PE的长,求出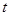 的值
的值
⑵通过 的解析式,求得M点的坐标,为求得
的解析式,求得M点的坐标,为求得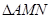 的周长最小,作点A 的关于x轴的对称点
的周长最小,作点A 的关于x轴的对称点 ,则经过
,则经过 、M两点的直线与x轴的交点即为点N
、M两点的直线与x轴的交点即为点N
⑶根据三角形的面积公式求得,若 为等腰三角形,分三种情况讨论
为等腰三角形,分三种情况讨论
 ⑶
⑶ ,①PQ=PC 则t=
,①PQ=PC 则t= ,②CP=CQ 则 t=4,
,②CP=CQ 则 t=4,③QC=QP 则 t=
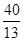 解析:
解析:解:⑴∵B、C在x轴上且抛物线经过B、C两点
∴令
 且
且 >0
>0 ∴
 即B(-2,0)、C(8,0)
即B(-2,0)、C(8,0)在Rt
 , OA=6,OC=8, ∴AC=10
, OA=6,OC=8, ∴AC=10过点P作PE⊥AC,垂足为E,则易证
 ∽
∽
∴
 ∴
∴ ∴
∴
当P为圆心,OP 为半径的圆与
 相切时,即PE=OP
相切时,即PE=OP∴
 则
则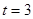 (3分)
(3分)⑵抛物线的对称轴为

直线
 经过A(0,6)、C(8,0), 易求
经过A(0,6)、C(8,0), 易求 的解析式为
的解析式为 ∴M(3,
∴M(3,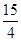 )
)为求得
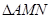 的周长最小,作点A 的关于x轴的对称点
的周长最小,作点A 的关于x轴的对称点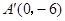
则经过
 、M两点的直线与x轴的交点即为点N
、M两点的直线与x轴的交点即为点N∴直线
 M的解析式为
M的解析式为 ∴N(
∴N( (6分)
(6分)⑶
 与
与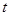 的函数关系式为
的函数关系式为
若
 为等腰三角形,分三种情况:
为等腰三角形,分三种情况:①PQ=PC 则t=

②CP=CQ 则 t=4
③QC=QP 则 t=
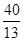 (9分)
(9分)⑴由已知求得B、C两点的坐标,过点P作PE⊥AC,垂足为E,证得
 ∽
∽ ,得出PE的长,求出
,得出PE的长,求出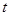 的值
的值⑵通过
 的解析式,求得M点的坐标,为求得
的解析式,求得M点的坐标,为求得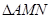 的周长最小,作点A 的关于x轴的对称点
的周长最小,作点A 的关于x轴的对称点 ,则经过
,则经过 、M两点的直线与x轴的交点即为点N
、M两点的直线与x轴的交点即为点N⑶根据三角形的面积公式求得,若
 为等腰三角形,分三种情况讨论
为等腰三角形,分三种情况讨论 
练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
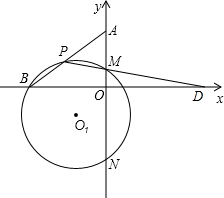
 交直线
交直线
 为何值时,
为何值时, 是
是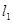 交直线
交直线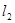 于
于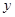 轴上一点
轴上一点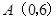 ,交
,交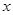 轴上另一点
轴上另一点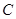 ,
,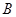 ,二次函数
,二次函数 (
(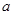 >0)的图像过点
>0)的图像过点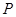 是线段
是线段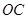 上由
上由 向
向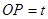 (1<
(1<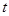 <8)。
<8)。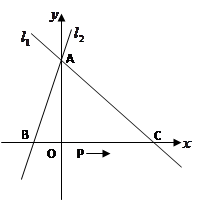
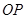 为半径的圆与
为半径的圆与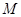 ,请在
,请在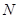 ,使
,使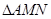 的周长最小;
的周长最小; 是
是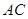 上由
上由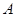 移动的一动点,且
移动的一动点,且 ,若
,若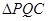 的面积为
的面积为 ,求
,求 交直线
交直线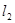 于
于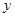 轴上一点
轴上一点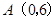 ,交
,交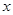 轴上另一点
轴上另一点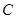 ,
, ,二次函数
,二次函数 (
(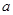 >0)的图像过点
>0)的图像过点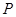 是线段
是线段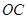 上由
上由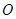 向
向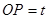 (1<
(1<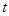 <8)。
<8)。
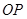 为半径的圆与
为半径的圆与 ,请在
,请在 ,使
,使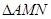 的周长最小;
的周长最小;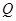 是
是 上由
上由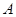 移动的一动点,且
移动的一动点,且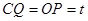 ,若
,若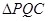 的面积为
的面积为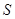 ,求
,求