题目内容
已知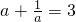 ,求
,求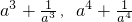 .
.
解:∵a+ =3,
=3,
∴(a+ )2=9,即a2+
)2=9,即a2+ =7,
=7,
∴(a+ )(a2+
)(a2+ )=21,即a3+a+
)=21,即a3+a+ +
+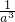 =21,
=21,
∴a3+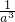 =21-3=18;
=21-3=18;
∵(a+ )(a3+
)(a3+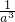 )=54,即a4+a2+
)=54,即a4+a2+ +
+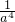 =54,
=54,
∴a4+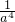 =54-7=47.
=54-7=47.
分析:先把a+ =3两边平方得到a2+
=3两边平方得到a2+ =7,然后用(a+
=7,然后用(a+ )(a2+
)(a2+ )可计算出a3+
)可计算出a3+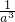 的值,用(a+
的值,用(a+ )(a3+
)(a3+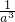 )可计算出a4+
)可计算出a4+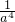 的值.
的值.
点评:本题考查了完全平方公式:(a+b)2=a2+2ab+b2.
 =3,
=3,∴(a+
 )2=9,即a2+
)2=9,即a2+ =7,
=7,∴(a+
 )(a2+
)(a2+ )=21,即a3+a+
)=21,即a3+a+ +
+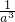 =21,
=21,∴a3+
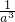 =21-3=18;
=21-3=18;∵(a+
 )(a3+
)(a3+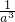 )=54,即a4+a2+
)=54,即a4+a2+ +
+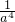 =54,
=54,∴a4+
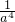 =54-7=47.
=54-7=47.分析:先把a+
 =3两边平方得到a2+
=3两边平方得到a2+ =7,然后用(a+
=7,然后用(a+ )(a2+
)(a2+ )可计算出a3+
)可计算出a3+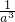 的值,用(a+
的值,用(a+ )(a3+
)(a3+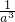 )可计算出a4+
)可计算出a4+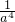 的值.
的值.点评:本题考查了完全平方公式:(a+b)2=a2+2ab+b2.

练习册系列答案
相关题目
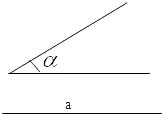 19、作图:以∠a顶角,线段a为腰作等腰三角形(要求写出已知,求作,不写作法和证明,保留作图痕迹.)
19、作图:以∠a顶角,线段a为腰作等腰三角形(要求写出已知,求作,不写作法和证明,保留作图痕迹.)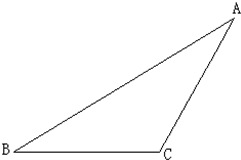

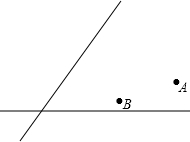 随着生活水平的提升,人们日益增强了卫生意识,如图所示,A,B均为市内住宅小区,旁边有两条相交的公路,环保公司增建一垃圾回收站P,为方便起见,要使得回收站P到两公路的距离相等,且到两个小区A,B的距离也相等,请在原图上利用尺规作图作出回收站P的位置.(要求:不写已知,求作、作法和结论,保留作图痕迹)
随着生活水平的提升,人们日益增强了卫生意识,如图所示,A,B均为市内住宅小区,旁边有两条相交的公路,环保公司增建一垃圾回收站P,为方便起见,要使得回收站P到两公路的距离相等,且到两个小区A,B的距离也相等,请在原图上利用尺规作图作出回收站P的位置.(要求:不写已知,求作、作法和结论,保留作图痕迹) 重庆园博园区内,有一块四边形草坪ABCD,需在其内部安置一个景观灯P,使点P到边BA、BC的距离相等,并且要求景观灯P到点C的距离等于线段CD的长.请作出景观灯P的位置.(要求:尺规作图,保留作图痕迹,不写出已知、求作、作法、结论和证明).
重庆园博园区内,有一块四边形草坪ABCD,需在其内部安置一个景观灯P,使点P到边BA、BC的距离相等,并且要求景观灯P到点C的距离等于线段CD的长.请作出景观灯P的位置.(要求:尺规作图,保留作图痕迹,不写出已知、求作、作法、结论和证明).