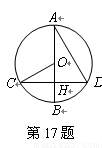
题目内容
如图,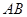 为
为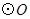 的直径,弦
的直径,弦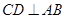 于点
于点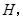 连结
连结 若
若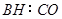
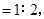
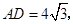 则
则 的周长等于
的周长等于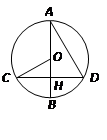
 解析:
解析:∵半径OB⊥CD, ∴ 弧BC = 弧BD ,CH=DH;(垂径定理)
∵BH:CO=1:2, ∴BH=OH=
 OC;
OC;在Rt△OCH中,OH=
 OC, ∴∠COH=60°;
OC, ∴∠COH=60°;∵ 弧BC = 弧BD , ∴∠DAH=
 ∠COH=30°;(圆周角定理)
∠COH=30°;(圆周角定理)在Rt△AHD中,∠DAH=30°,AD=4
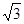 ,则DH=CH=2
,则DH=CH=2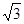 ;
;在Rt△OCH中,∠COH=60°,CH=2
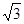 ,则OC=4.
,则OC=4.∴⊙O的周长为8π.

练习册系列答案
相关题目
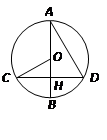
 为
为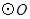 的直径,弦
的直径,弦 于点
于点 连结
连结 若
若

 则
则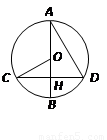
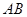 为
为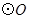 的直径,弦
的直径,弦 于点
于点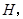 连结
连结 若
若

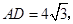 则
则