题目内容
【题目】如图,在等腰![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 在
在![]() 上,
上,![]() ,将线段
,将线段![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得到
得到![]() ,连接
,连接![]() ,然后把
,然后把![]() 沿着
沿着![]() 翻折得到
翻折得到![]() ,连接
,连接![]() ,
,![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() 的长为( )
的长为( )

A.![]() B.
B.![]() C.2D.
C.2D.![]()
【答案】B
【解析】
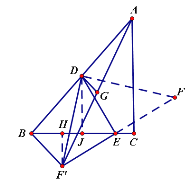
根据D,G为中点,要求出DG,通过求出BF’即可,作DJ⊥BC,F’H⊥BC,求出DJ、JE的长,再根据等腰直角三角形的性质得到△DJE≌△EF’H,求出HF’,HE,得到BH的长,再根据勾股定理求出BF’故可求解.
在等腰![]() 中,
中,![]() ,
,![]() ,
,
∴AC=BC=10,点![]() 在
在![]() 上,
上,![]() ,
,
∴BE=8,
依题意可知△DEF’为等腰直角三角形,
∴DE=EF’
作DJ⊥BC,F’H⊥BC,
∵D为AB中点,
∴J为BC中点,
∴DJ=![]() AC=5,JC=5,JE=5-2=3
AC=5,JC=5,JE=5-2=3
∵∠DEF’=90°,
∴∠DEJ+∠HEF’=90°,
又∠HF’E+∠HEF’=90°
∴∠DEJ=∠HF’E,
又DE=EF’
∴△DJE≌△EF’H(AAS)
∴HF’=JE=3,HE=DJ=5,
∴BH=8-5=3,
∴BF’=![]()
∵D,G分别为AB,AF’的中点,
∴DG=![]() BF’=
BF’=![]()
故选B.

【题目】车间有20名工人,某一天他们生产的零件个数统计如下表:
生产零件的个数(个) | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
工人人数(人) | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
(1)求这一天20名工人生产零件的平均个数;
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?
【题目】全民健身运动已成为一种时尚,为了了解我市居民健身运动的情况,某健身馆的工作人员开展了一项问卷调查,问卷包括五个项目:A:健身房运动;B:跳广场舞;C:参加暴走团;D:散布;E:不运动.
以下是根据调查结果绘制的统计图表的一部分.
运动形式 | A | B | C | D | E |
人数 | 12 | 30 | m | 54 | 9 |
请你根据以上信息,回答下列问题:
(1)接受问卷调查的共有 人,图表中的m= ,n= ;
(2)统计图中,A类所对应的扇形圆心角的度数为 ;
(3)根据调查结果,我市市民最喜爱的运动方式是 ,不运动的市民所占的百分比是 ;
(4)我市碧沙岗公园是附近市民喜爱的运动场所之一,每晚都有“暴走团”活动,若最邻近的某社区约有1500人,那么估计一下该社区参加碧沙岗“暴走团”的大约有多少人?