题目内容
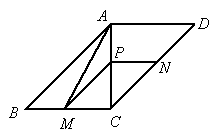
(2006,温州)如图,在平行四边形ABCD中,对角线AC⊥BC,AC=BC=2.动点P从点A出发,尚AC向终点C移动,过点P分别作PM∥AB交BC于M,PN∥AD交DC于N,连结AM,设AP=x.
(1)四边形PMCN的形状有可能是菱形吗?请说明理由.
(2)当x为何值时,四边形PMCN的面积与△ABM的面积相等?
答案:略
解析:
解析:
|
解: (1)四边形PMCN不可能是菱形.点 P在运动过程中,△PCM始终是一个直角三角形,∴斜边 PM大于直角边MC,∴四边形 PMCN不可能是菱形.(2) ∵PM∥AB,AC⊥BC,AC=BC=2,∴∠ PMC=∠ABC=∠BAC=∠MPC,∴ CM=CP=2-x,∴ BM=x.∴ 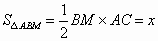 . .
由已知可得四边形 PMCN是平行四边形,∴ 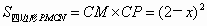 . .
若 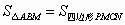 ,则 ,则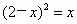 . .
解得 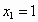 , ,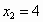 . .
∴当 x=1时,四边形PMCN的面积与△ABM的面积相等. |

练习册系列答案
相关题目
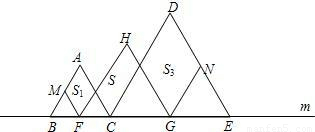
 CE,F、G分别是BC、CE的中点,FM∥AC,GN∥DC.设图中三个平行四边形的面积依次是S1,S,S3,若S1+S3=10,则S= .
CE,F、G分别是BC、CE的中点,FM∥AC,GN∥DC.设图中三个平行四边形的面积依次是S1,S,S3,若S1+S3=10,则S= .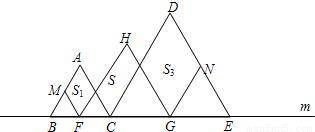

 CE,F、G分别是BC、CE的中点,FM∥AC,GN∥DC.设图中三个平行四边形的面积依次是S1,S,S3,若S1+S3=10,则S= .
CE,F、G分别是BC、CE的中点,FM∥AC,GN∥DC.设图中三个平行四边形的面积依次是S1,S,S3,若S1+S3=10,则S= .