题目内容
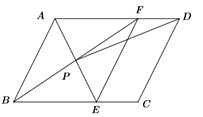
【题目】如图,在平行四边形ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.
(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求PD.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由四边形ABCD是平行四边形,得到AD∥BC,从而得到∠AFB=∠FBE,再由∠ABF=∠FBE,推出∠ABF=∠AFB,于是得到AB=AF,同理得出AB=BE,于是得出结论;
(2)由菱形的性质得出AE⊥BF,得到∠ABF=30°,∠BAP=∠FAP=60°从而得出AP=2,过点P作PM⊥AD于M,得到PM=![]() ,AM=1,DM=5,然后利用勾股定理求PD即可.
,AM=1,DM=5,然后利用勾股定理求PD即可.
(1)∵四边形ABCD是平行四边形,∴AD∥BC,∴∠AFB=∠FBE.
∵∠ABF=∠FBE,∴∠ABF=∠AFB,∴AB=AF,同理AB=BE,∴四边形ABEF是菱形;
(2)∵四边形ABEF是菱形,∴AE⊥BF.
∵∠ABC=60°,∴∠ABF=30°,∠BAP=∠FAP=60°.
∵AB=4,∴AP=2,如图,过点P作PM⊥AD于M,∴PM=![]() ,AM=1.
,AM=1.
∵AD=6,∴DM=5,∴PD=![]() .
.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中正确的是( )
A. 抛物线与x轴的一个交点为(4,0)
B. 函数y=ax2+bx+c的最大值为6
C. 抛物线的对称轴是x=![]()
D. 在对称轴右侧,y随x增大而增大