题目内容
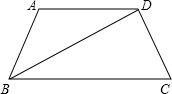 如图梯形ABCD中,AD∥BC,AB=AD=CD,BD⊥CD,求∠C的度数.
如图梯形ABCD中,AD∥BC,AB=AD=CD,BD⊥CD,求∠C的度数.
分析:由AB=AD=CD,可知∠ABD=∠ADB,又AD∥BC,可推得BD为∠B的平分线,而由题可知梯形ABCD为等腰梯形,则∠B=∠C,那么在RT△BDC中,
∠C+∠C=90°,可求得∠C=60°.
| 1 |
| 2 |
解答:解:∵AB=AD=CD
∴∠ABD=∠ADB
∵AD∥BC
∴∠ADB=∠DBC
∴∠ABD=∠DBC
∴BD为∠B的平分线
∵AD∥BC,AB=AD=CD
∴梯形ABCD为等腰梯形
∴∠B=∠C
∵BD⊥CD
∴
∠C+∠C=90°
∴∠C=60°
∴∠ABD=∠ADB
∵AD∥BC
∴∠ADB=∠DBC
∴∠ABD=∠DBC
∴BD为∠B的平分线
∵AD∥BC,AB=AD=CD
∴梯形ABCD为等腰梯形
∴∠B=∠C
∵BD⊥CD
∴
| 1 |
| 2 |
∴∠C=60°
点评:先根据已知条件可知四边形为等腰梯形,然后根据等腰梯形的性质和已知条件求解.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
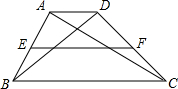 如图梯形ABCD中,AD∥BC,AB=DC=2,∠ABC=60°,且BD⊥AC,EF是梯形的中位线,求EF的长.
如图梯形ABCD中,AD∥BC,AB=DC=2,∠ABC=60°,且BD⊥AC,EF是梯形的中位线,求EF的长.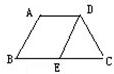 20、如图梯形ABCD中,∠B=60°,AB=5cm,将AB向右平移到点D,交BC于E,那么DE=
20、如图梯形ABCD中,∠B=60°,AB=5cm,将AB向右平移到点D,交BC于E,那么DE=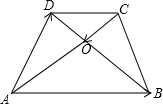
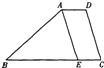 15、如图梯形ABCD中,AD∥BC,AE∥DC,AD=5cm,梯形ABCD的周长为60cm,则△ABE的周长为( )
15、如图梯形ABCD中,AD∥BC,AE∥DC,AD=5cm,梯形ABCD的周长为60cm,则△ABE的周长为( )