题目内容
 如图梯形ABCD中,AD∥BC,AB=DC=2,∠ABC=60°,且BD⊥AC,EF是梯形的中位线,求EF的长.
如图梯形ABCD中,AD∥BC,AB=DC=2,∠ABC=60°,且BD⊥AC,EF是梯形的中位线,求EF的长.
分析:根据题意先作出辅助线,利用梯形中位线定理求解.
解答: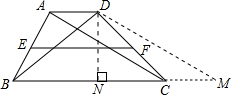 解:如图:过点D作DM∥AC,交BC的延长线于点M,DN⊥BC,垂足为N,
解:如图:过点D作DM∥AC,交BC的延长线于点M,DN⊥BC,垂足为N,
∵AB=DC=2,∠ABC=60°,
∴∠NDC=30°,NC=1,
∴DN=
,
∵BD⊥AC,
∴BD⊥DM,
∴△BDM与梯形ABCD的面积相等,AD+BC=BM=2
∵EF是梯形的中位线,
∴EF=
BM=
.
 解:如图:过点D作DM∥AC,交BC的延长线于点M,DN⊥BC,垂足为N,
解:如图:过点D作DM∥AC,交BC的延长线于点M,DN⊥BC,垂足为N,∵AB=DC=2,∠ABC=60°,
∴∠NDC=30°,NC=1,
∴DN=
| 3 |
∵BD⊥AC,
∴BD⊥DM,
∴△BDM与梯形ABCD的面积相等,AD+BC=BM=2
| 3 |
∵EF是梯形的中位线,
∴EF=
| 1 |
| 2 |
| 3 |
点评:考查了梯形中位线定理.当等腰梯形的对角线互相垂直时,平移一条腰构造等腰直角三角形是常用的辅助线作法.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
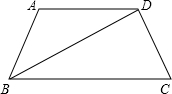 如图梯形ABCD中,AD∥BC,AB=AD=CD,BD⊥CD,求∠C的度数.
如图梯形ABCD中,AD∥BC,AB=AD=CD,BD⊥CD,求∠C的度数. 20、如图梯形ABCD中,∠B=60°,AB=5cm,将AB向右平移到点D,交BC于E,那么DE=
20、如图梯形ABCD中,∠B=60°,AB=5cm,将AB向右平移到点D,交BC于E,那么DE=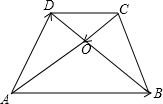
 15、如图梯形ABCD中,AD∥BC,AE∥DC,AD=5cm,梯形ABCD的周长为60cm,则△ABE的周长为( )
15、如图梯形ABCD中,AD∥BC,AE∥DC,AD=5cm,梯形ABCD的周长为60cm,则△ABE的周长为( )