题目内容
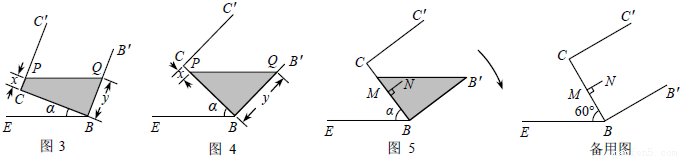
一透明的敞口正方体容器ABCD-![]() 装有一些液体,棱AB始终在水平桌面上,容器底部的倾斜角为α(∠CBE=α,如图①所示).
装有一些液体,棱AB始终在水平桌面上,容器底部的倾斜角为α(∠CBE=α,如图①所示).
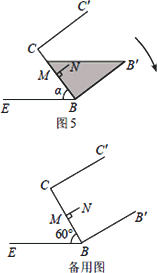
探究如图①,液面刚好过棱CD,并与棱B![]() 交于点Q,此时液体的形状为直三棱柱,其三视图及尺寸如图②所示.解决问题:
交于点Q,此时液体的形状为直三棱柱,其三视图及尺寸如图②所示.解决问题:

(1)CQ与BE的位置关系是________,BQ的长是________dm;
(2)求液体的体积;(参考算法:直棱柱体积V液=底面积SBCQ×高AB)
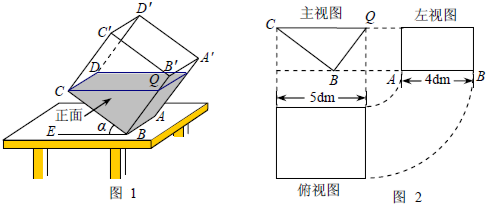
(3)求α的度数.(注:sin49°=cos41°=![]() ,tan37°=
,tan37°=![]() )
)
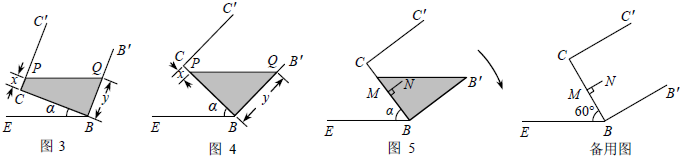
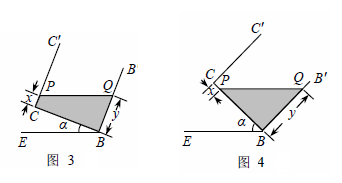
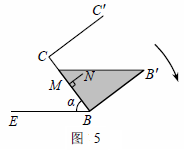
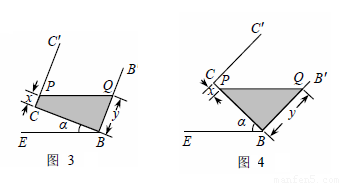
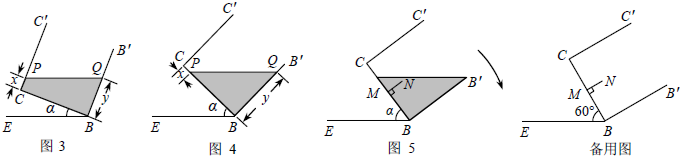
拓展在图①的基础上,以棱AB为轴将容器向左或向右旋转,但不能使液体溢出,图③或图④是其正面示意图.若液面与棱![]() C或CB交于点P,设PC=x,BQ=y.分别就图③和图④求y与x的函数关系式,并写出相应的α的范围.
C或CB交于点P,设PC=x,BQ=y.分别就图③和图④求y与x的函数关系式,并写出相应的α的范围.
[温馨提示:下页还有题!]

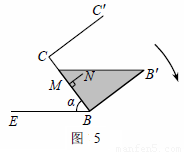
延伸在图④的基础上,于容器底部正中间位置,嵌入一平行于侧面的长方形隔板(厚度忽略不计),得到图⑤,隔板高NM=1 dm,BM=CM,NM⊥BC.继续向右缓慢旋转,当α=60°时,通过计算,判断溢出容器的液体能否达到4 dm3.
答案:

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 ,tan37°=
,tan37°=
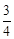 ,tan37°=
,tan37°=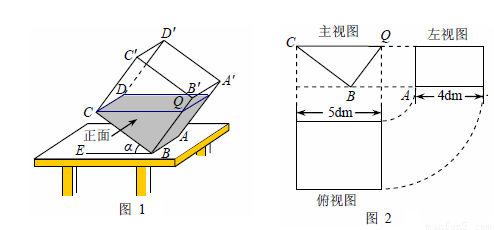
 ,tan37°=
,tan37°=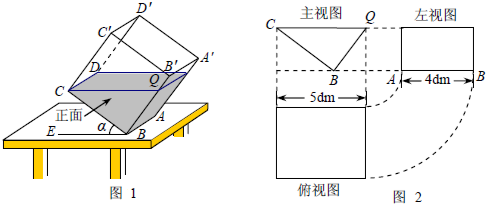
 ,tan37°=
,tan37°= )
)