题目内容
某地生产一种绿色蔬菜,在市场上直接销售,每吨利润为1000元,经粗加工后每吨可获利4000元,经精加工后每吨获利8000元,当地一家农工商公司收购这种蔬菜140吨.
| 每天加工数量 | 利润 | |
| 粗加工 | 10吨/天 | 4000元/吨 |
| 精加工 | 8吨/天 | 8000元/吨 |
方案一:将蔬菜全部进行粗加工;
方案二:尽可能多地对蔬菜进行精加工,没来得及加工的蔬菜在市场上全部销售;
方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好在15天内完成.
你认为选择哪种方案获利最多,为什么?
解:选择第二种方案获利最多.
方案一:因为每天粗加工10吨,140吨可以在15天内加工完.
总利润W1=4000×140=560000(元);
方案二:因为每天精加工8吨,15天可以加工120吨,其余20吨直接销售.
总利润W2=120×8000+20×1000=980000(元);
方案三:设15天内精加工蔬菜x吨,粗加工蔬菜y吨,
依题意得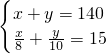 ,
,
解得: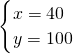 ,
,
总利润W3=40×8000+100×4000=720000(元),
综合以上三种方案的利润情况,知W1<W3<W2,所以第二种方案获利最多.
分析:要判定哪一种方案获利最多,只要求出每种方案获利多少,再进行比较就可以了,第三种方案中有多少粗加工、有多少细加工需要列二元一次方程组来解决.
点评:本题考查了二元一次方程组的应用,解答此题的关键是列出二元一次方程组解决方案三,求出获利多少,再与方案一,方案二比较.
方案一:因为每天粗加工10吨,140吨可以在15天内加工完.
总利润W1=4000×140=560000(元);
方案二:因为每天精加工8吨,15天可以加工120吨,其余20吨直接销售.
总利润W2=120×8000+20×1000=980000(元);
方案三:设15天内精加工蔬菜x吨,粗加工蔬菜y吨,
依题意得
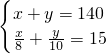 ,
,解得:
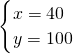 ,
,总利润W3=40×8000+100×4000=720000(元),
综合以上三种方案的利润情况,知W1<W3<W2,所以第二种方案获利最多.
分析:要判定哪一种方案获利最多,只要求出每种方案获利多少,再进行比较就可以了,第三种方案中有多少粗加工、有多少细加工需要列二元一次方程组来解决.
点评:本题考查了二元一次方程组的应用,解答此题的关键是列出二元一次方程组解决方案三,求出获利多少,再与方案一,方案二比较.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目