题目内容
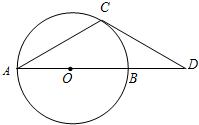 (2010•东营)如图,AB是⊙O的直径,点D在AB的延长线上,点C在⊙O上,CA=CD,∠CDA=30°.
(2010•东营)如图,AB是⊙O的直径,点D在AB的延长线上,点C在⊙O上,CA=CD,∠CDA=30°.(1)判断直线CD与⊙O的位置关系为
相切
相切
;(2)若⊙O的半径为5,则点A到CD所在直线的距离为
7.5
7.5
.分析:(1)连接OC,证明∠OCD=90°,从而判断CD与⊙O相切.易证∠A=30°,∠COD=60°.所以∠OCD=90°.得证;
(2)作AE⊥DC,交DC的延长线于E点.运用三角函数知识,在△OCD中求OD,从而知AD长度;在△ADE中求AE,得解.
(2)作AE⊥DC,交DC的延长线于E点.运用三角函数知识,在△OCD中求OD,从而知AD长度;在△ADE中求AE,得解.
解答: 解:(1)∵△ACD是等腰三角形,∠D=30°.∴∠CAD=∠CDA=30°. (1分)
解:(1)∵△ACD是等腰三角形,∠D=30°.∴∠CAD=∠CDA=30°. (1分)
连接OC.
∵AO=CO,∴△AOC是等腰三角形. (2分)
∴∠CAO=∠ACO=30°,∴∠COD=60°. (3分)
在△COD中,
又∵∠CDO=30°,∴∠DCO=90°. (4分)
∴CD是⊙O的切线,即直线CD与⊙O相切. (5分)
(2)过点A作AE⊥CD,垂足为E. (6分)
在Rt△COD中,∵∠CDO=30°,∴OD=2OC=10.AD=AO+OD=15. (7分)
在Rt△ADE中,∵∠EDA=30°,∴点A到CD边的距离为:AE=AD•sin30°=7.5.(9分)
 解:(1)∵△ACD是等腰三角形,∠D=30°.∴∠CAD=∠CDA=30°. (1分)
解:(1)∵△ACD是等腰三角形,∠D=30°.∴∠CAD=∠CDA=30°. (1分)连接OC.
∵AO=CO,∴△AOC是等腰三角形. (2分)
∴∠CAO=∠ACO=30°,∴∠COD=60°. (3分)
在△COD中,
又∵∠CDO=30°,∴∠DCO=90°. (4分)
∴CD是⊙O的切线,即直线CD与⊙O相切. (5分)
(2)过点A作AE⊥CD,垂足为E. (6分)
在Rt△COD中,∵∠CDO=30°,∴OD=2OC=10.AD=AO+OD=15. (7分)
在Rt△ADE中,∵∠EDA=30°,∴点A到CD边的距离为:AE=AD•sin30°=7.5.(9分)
点评:此题考查了切线的判定、解直角三角形等知识点,难度中等.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目