题目内容
(2010•东营)如图,点C是线段AB上的一个动点,△ACD和△BCE是在AB同侧的两个等边三角形,DM,EN分别是△ACD和△BCE的高,点C在线段AB上沿着从点A向点B的方向移动(不与点A,B重合),连接DE,得到四边形DMNE.这个四边形的面积变化情况为( )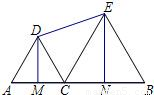
A.逐渐增大
B.逐渐减小
C.始终不变
D.先增大后变小
【答案】分析:易得此四边形为直角梯形,AB的长度一定,那么直角梯形的高为AB的长度的一半,上下底的和也一定,所以面积不变.
解答:解:当点C在线段AB上沿着从点A向点B的方向移动时,
根据等边三角形的性质,等边△ACD和△BCE的高DM和EN的和不会改变,
即DM+EN=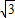 MC+
MC+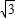 CN=
CN=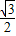 AC+
AC+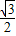 CB=
CB=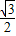 AB,
AB,
而且MN的长度也不会改变,即MN= AC+
AC+ CB=
CB= AB.
AB.
∴四边形DMNE面积=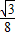 AB2,
AB2,
∴面积不会改变.
故选C.
点评:考查等边三角形的性质和梯形的面积公式.
解答:解:当点C在线段AB上沿着从点A向点B的方向移动时,
根据等边三角形的性质,等边△ACD和△BCE的高DM和EN的和不会改变,
即DM+EN=
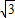 MC+
MC+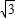 CN=
CN=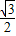 AC+
AC+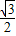 CB=
CB=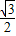 AB,
AB,而且MN的长度也不会改变,即MN=
 AC+
AC+ CB=
CB= AB.
AB.∴四边形DMNE面积=
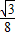 AB2,
AB2,∴面积不会改变.
故选C.
点评:考查等边三角形的性质和梯形的面积公式.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
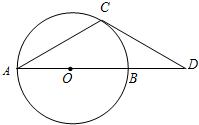 (2010•东营)如图,AB是⊙O的直径,点D在AB的延长线上,点C在⊙O上,CA=CD,∠CDA=30°.
(2010•东营)如图,AB是⊙O的直径,点D在AB的延长线上,点C在⊙O上,CA=CD,∠CDA=30°.