题目内容
将函数y=
| ||
| 3 |
 别与y轴交于O、A两点,与直线x=-
别与y轴交于O、A两点,与直线x=-| 3 |
(1)求这个新函数的解析式;
(2)判断以A、B、C、O四点为顶点的四边形形状,并说明理由;
(3)若(2)中的四边形(不包括边界)始终覆盖着二次函数y=x2-2bx+b2+
| 1 |
| 2 |
分析:(1)依题意,根据二次函数的性质可知函数y=
x的图象向上平移2个单位得出一个新函数为y=
x+2.
(2)依题意得出AB∥CO,BC∥AO推出四边形AOCB为平行四边形,然后由勾股定理可得AB=AO可推出平行四边形AOCB为菱形.
(3)把二次函数化为顶点式后可得抛物线顶点在直线y=
上移动.分别把点A、B代入二次函数求出b的取值范围.
| ||
| 3 |
| ||
| 3 |
(2)依题意得出AB∥CO,BC∥AO推出四边形AOCB为平行四边形,然后由勾股定理可得AB=AO可推出平行四边形AOCB为菱形.
(3)把二次函数化为顶点式后可得抛物线顶点在直线y=
| 1 |
| 2 |
解答:解:(1)y=
x+2.(2分)
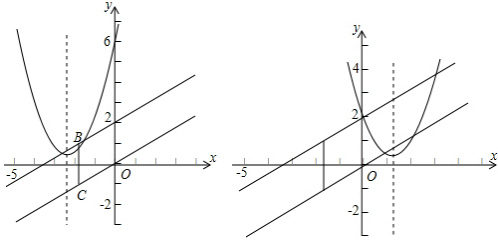
(2)答:四边形AOCB为菱形(3分)
由题意可得AB∥CO,BC∥AO,AO=2
∴四边形AOCB为平行四边形(4分)
易得A(0,2),B(-
,1).
由勾股定理可得AB=2,
∴AB=AO(5分)
∴平行四边形AOCB为菱形(6分)
(3)二次函数y=x2-2bx+b2+
,
化为顶点式为:y=(x-b)2+
(7分)
∴抛物线顶点在直线y=
上移动
假设四边形的边界可以覆盖到二次函数,
则B点和A点分别是二次函数与四边形接触的边界点
将B(-
,1),
代入二次函数,
解得b=-
-
,b=-
+
(不合题意,舍去)(8分)
将A(0,2),代入二次函数,
解得b=
,b=-
(不合题意,舍去)(9分)
所以实数b的取值范围:-
-
<b<
.(10分)
| ||
| 3 |

(2)答:四边形AOCB为菱形(3分)
由题意可得AB∥CO,BC∥AO,AO=2
∴四边形AOCB为平行四边形(4分)
易得A(0,2),B(-
| 3 |
由勾股定理可得AB=2,
∴AB=AO(5分)
∴平行四边形AOCB为菱形(6分)
(3)二次函数y=x2-2bx+b2+
| 1 |
| 2 |
化为顶点式为:y=(x-b)2+
| 1 |
| 2 |
∴抛物线顶点在直线y=
| 1 |
| 2 |
假设四边形的边界可以覆盖到二次函数,
则B点和A点分别是二次函数与四边形接触的边界点
将B(-
| 3 |
代入二次函数,
解得b=-
| 3 |
| ||
| 2 |
| 3 |
| ||
| 2 |
将A(0,2),代入二次函数,
解得b=
| ||
| 2 |
| ||
| 2 |
所以实数b的取值范围:-
| 3 |
| ||
| 2 |
| ||
| 2 |
点评:本题考查的是二次函数与图象相结合的有关知识,难度较大.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
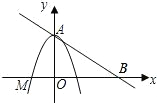 四边形是平行四边形.
四边形是平行四边形. 已知:将函数
已知:将函数 、B,线段AB为边在第一象限内作等边△ABC.
、B,线段AB为边在第一象限内作等边△ABC.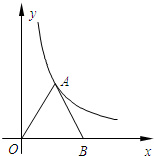 (2013•婺城区一模)如图,点A在反比例函数
(2013•婺城区一模)如图,点A在反比例函数