题目内容
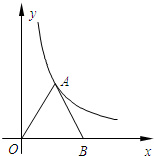（2013•婺城区一模）如图，点A在反比例函数y=3
| ||
| x |
（1）A点坐标为
（
，3）
| 3 |
（
，3）
；| 3 |
（2）将△OAB绕其中心（等边三角形外接圆的圆心）旋转60°，得到△O′A′B′．则A，O′两点间的距离等于
2或4
2或4
．分析：（1）根据等边三角形的性质，可设点A的坐标为（a，
a），代入反比例函数解析式可得出a的值，继而得出点A的坐标．
（2）分两种情况讨论，①顺时针旋转，②逆时针旋转，依次得出两点的距离即可．
| 3 |
（2）分两种情况讨论，①顺时针旋转，②逆时针旋转，依次得出两点的距离即可．
解答：解：（1）∵△ABC是等边三角形，
∴可设点A的坐标为（a，
a），
将点A（a，
a）代入反比例函数可得：
a=
，
解得：a1=
，a2=-
（舍去），
∴点A的坐标为（
，3）．
（2）
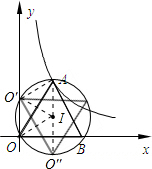
由（1）可得等边三角形ABC的边长为2
，外接圆的半径R=2，
①若顺时针旋转，此时点O位于点O'的位置，
∵旋转角为60°，IO'=IA=R，
∴△AIO'是等边三角形，
∴AO'=R=2；
②若逆时针旋转，此时点O位于O''位置，则此时AO''=2R=4．
综上可得O′、A两点间的距离等于2或4．
故答案为：（
，3）、2或4．
∴可设点A的坐标为（a，
| 3 |
将点A（a，
| 3 |
| 3 |
3
| ||
| a |
解得：a1=
| 3 |
| 3 |
∴点A的坐标为（
| 3 |
（2）
由（1）可得等边三角形ABC的边长为2
| 3 |
①若顺时针旋转，此时点O位于点O'的位置，
∵旋转角为60°，IO'=IA=R，
∴△AIO'是等边三角形，
∴AO'=R=2；
②若逆时针旋转，此时点O位于O''位置，则此时AO''=2R=4．
综上可得O′、A两点间的距离等于2或4．
故答案为：（
| 3 |
点评：本题考查了反比例函数综合题，涉及了等边三角形的性质、旋转的性质及圆的知识，难点在第二问，结合圆进行求解是关键，注意分类讨论，不要漏解，此题难度较大．
练习册系列答案
相关题目
（2013•婺城区一模）如图是二次函数y=ax2+bx的图象，若一元二次方程ax2+bx+m=0有实数根，则实数m的最大值为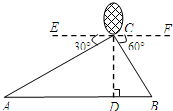
（2013•婺城区一模）热气球C从建筑物A的底部沿直线开始斜着往上飞行，当飞行了180米距离时到达如图中的位置，此时在热气球上测得两建筑物A，B底部的俯角分别为30°和60°﹒若此时热气球在地面的正投影D与点A，B在同一直线上﹒