题目内容
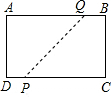
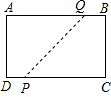已知如图，长方形ABCD，AB=8，BC=6，若将长方形顶点A、C重合折叠起来，则折痕PQ长为（ ）A、
| ||
| B、7 | ||
| C、8 | ||
D、
|
分析：由长方形顶点A、C重合折叠可知，AC与PQ相互垂直平分，不妨设AC与PQ相交于点O，再证得△POC相似△ADC，进一步利用三角形相似的性质解答即可．
解答：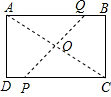
解：如图，AC与PQ相交于点O，OC=
AC=
=5，
∵顶点A、C重合，
∴AC与PQ相互垂直平分，
∴∠POC=90°，
而∠D=90°，∠OCP=∠DCA，
∴△POC∽△ADC，
∴
=
，
即PO=
=
，
得PO=
，
因此PQ=
．
故选A．
解：如图，AC与PQ相交于点O，OC=| 1 |
| 2 |
| 1 |
| 2 |
| AB2+BC2 |
∵顶点A、C重合，
∴AC与PQ相互垂直平分，
∴∠POC=90°，
而∠D=90°，∠OCP=∠DCA，
∴△POC∽△ADC，
∴
| PO |
| AD |
| OC |
| DC |
即PO=
| AD•OC |
| DC |
| 6×5 |
| 8 |
得PO=
| 15 |
| 4 |
因此PQ=
| 15 |
| 2 |
故选A．
点评：此题主要利用矩形的性质，对称的性质以及三角形相似的判定与性质解决问题．
练习册系列答案
相关题目
已知如图：长方形ABCD中，AB=3，BC=4，将△BCD沿BD翻折，点C落在点F处．
已知如图，长方形ABCD，AB=8，BC=6，若将长方形顶点A、C重合折叠起来，则折痕PQ长为
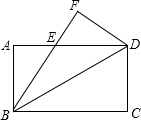已知如图：长方形ABCD中，AB=3，BC=4，将△BCD沿BD翻折，点C落在点F处．