题目内容
直线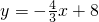 与X轴Y轴分别交于点M,N,如果点P在坐标轴上,以点P为圆心,
与X轴Y轴分别交于点M,N,如果点P在坐标轴上,以点P为圆心, 为半径的圆与直线
为半径的圆与直线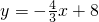 相切,则符合要求的点P个数可能为
相切,则符合要求的点P个数可能为
- A.1
- B.2
- C.3
- D.4
D
分析:由题中所述点P在坐标轴上,所以要分①当P1点在y轴上,并且在N点的下方;②当P2点在x轴上,并且在M点的左侧;③当P3点在x轴上,并且在M点的右侧;④当P4点在y轴上,并且在点N上方这四种情况讨论,再根据圆的性质及相切的条件,以及相似三角形的对应边成比例,从而求出每种情况的P点坐标.
解答:分以下几种情况讨论:
①当P1点在y轴上,并且在N点的下方时,设⊙P1与直线y=- x+4相切于点A,
x+4相切于点A,
连接P1A,则P1A⊥MN,
∴∠P1AN=∠MON=90°.
∵∠P1NA=∠MNO,
∴△P1AN∽△MON,
∴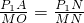
在Rt△OMN中,OM=6,ON=8,
∴MN=10.
又∵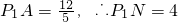 ,
,
∴P1点坐标是(0,4);
②当P2点在x轴上,并且在M点的左侧时,同理可得P2点坐标是(3,0);
③当P3点在x轴上,并且在M点的右侧时,设⊙P3与直线y=- x+4上切于点B,连接P3B.
x+4上切于点B,连接P3B.
则P3B⊥MN,∴△P3BM∽△MON,∴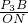 =
= ,
,
又ON=8,MN=10,P3B= ,
,
∴P3M=3,∴P3点坐标是(9,0);
④当P4点在y轴上,并且在点N上方时,同理可得P4N=4.
∴P4点坐标是(0,12).
综上,P点有(0,4),(3,0),(9,0),(0,12)共四个.
故选D.
点评:本题考查了一次函数的基本性质及直线与圆相切的有关知识,同时还考查了相似三角形的性质及分类讨论的思想,有一定的难度.
分析:由题中所述点P在坐标轴上,所以要分①当P1点在y轴上,并且在N点的下方;②当P2点在x轴上,并且在M点的左侧;③当P3点在x轴上,并且在M点的右侧;④当P4点在y轴上,并且在点N上方这四种情况讨论,再根据圆的性质及相切的条件,以及相似三角形的对应边成比例,从而求出每种情况的P点坐标.
解答:分以下几种情况讨论:
①当P1点在y轴上,并且在N点的下方时,设⊙P1与直线y=-
 x+4相切于点A,
x+4相切于点A,连接P1A,则P1A⊥MN,
∴∠P1AN=∠MON=90°.
∵∠P1NA=∠MNO,
∴△P1AN∽△MON,
∴
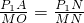
在Rt△OMN中,OM=6,ON=8,
∴MN=10.
又∵
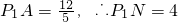 ,
,∴P1点坐标是(0,4);
②当P2点在x轴上,并且在M点的左侧时,同理可得P2点坐标是(3,0);
③当P3点在x轴上,并且在M点的右侧时,设⊙P3与直线y=-
 x+4上切于点B,连接P3B.
x+4上切于点B,连接P3B.则P3B⊥MN,∴△P3BM∽△MON,∴
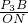 =
= ,
,又ON=8,MN=10,P3B=
 ,
,∴P3M=3,∴P3点坐标是(9,0);
④当P4点在y轴上,并且在点N上方时,同理可得P4N=4.
∴P4点坐标是(0,12).
综上,P点有(0,4),(3,0),(9,0),(0,12)共四个.
故选D.
点评:本题考查了一次函数的基本性质及直线与圆相切的有关知识,同时还考查了相似三角形的性质及分类讨论的思想,有一定的难度.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 与x轴y轴分别交于点A和点B,点B的坐标为(0,6)
与x轴y轴分别交于点A和点B,点B的坐标为(0,6)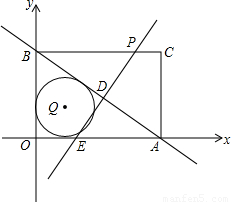
 与x轴y轴分别交于点A和点B,点B的坐标为(0,6)
与x轴y轴分别交于点A和点B,点B的坐标为(0,6)
 与x轴y轴分别交于点A和点B,点B的坐标为(0,6)
与x轴y轴分别交于点A和点B,点B的坐标为(0,6)
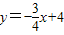 与x轴y轴分别交于点M,N,
与x轴y轴分别交于点M,N, 为半径的圆与直线y=-
为半径的圆与直线y=-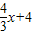 相切,求点P的坐标.
相切,求点P的坐标.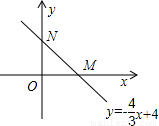
 与x轴y轴分别交于点E、F,点E的坐标为(-8,0),点A的坐标为(-6,0)。(1)求
与x轴y轴分别交于点E、F,点E的坐标为(-8,0),点A的坐标为(-6,0)。(1)求 的值;(2)若点P(
的值;(2)若点P( ,
, )是第二象限内的直线上的一个动点,在点P的运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;(3)探究:当点P运动到什么位置时,△OPA的面积为,并说明理由。
)是第二象限内的直线上的一个动点,在点P的运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;(3)探究:当点P运动到什么位置时,△OPA的面积为,并说明理由。