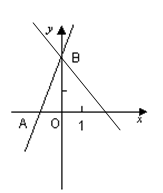
题目内容
如图,直线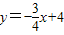 与x轴y轴分别交于点M,N,
与x轴y轴分别交于点M,N,(1)求MN两点的坐标;
(2)如果点A在线段ON上,将△NMA沿直线MA折叠,N点恰好落在x轴上的N′点,求直线MA的解析式;
(3)如果点P在坐标轴上,以点P为圆心,
 为半径的圆与直线y=-
为半径的圆与直线y=-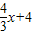 相切,求点P的坐标.
相切,求点P的坐标.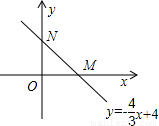
【答案】分析:(1)由直线解析式可以解得两坐标;
(2)由点A在线段ON上,将△NMA沿直线MA折叠,N点恰好落在x轴上的N′点,故知MN=MN′,求NN′的斜率就知道MA的斜率;
(3)分类讨论P在坐标轴上的情况.
解答:解:(1)M(3,0)N(0,4);
(2)∵点A在线段ON上,将△NMA沿直线MA折叠,N点恰好落在x轴上的N′点,
∴MN=MN′,
∴N′(-2,0),
∴kNN′=2,
∴kMA=- ,
,
∴ ;
;
(3)第一种情况:当P1在y轴上且在点N下方时,P1坐标是(0,0);
第二种情况:当P2在x轴且在M点的左侧时,P2坐标是(0,0);
第三种情况:当P3在x轴且在M点右侧时,P3坐标是(6,0);
第四种情况:当P4在y轴且在点N上方时,P4的坐标是(0,8),
综上,P坐标是(0,0)(6,0)(0,8).
点评:本题主要考查一次函数的应用,能够根据题意中的等量关系建立函数关系式;能够根据函数解析式求得对应的x的值.
(2)由点A在线段ON上,将△NMA沿直线MA折叠,N点恰好落在x轴上的N′点,故知MN=MN′,求NN′的斜率就知道MA的斜率;
(3)分类讨论P在坐标轴上的情况.
解答:解:(1)M(3,0)N(0,4);
(2)∵点A在线段ON上,将△NMA沿直线MA折叠,N点恰好落在x轴上的N′点,
∴MN=MN′,
∴N′(-2,0),
∴kNN′=2,
∴kMA=-
 ,
,∴
 ;
;(3)第一种情况:当P1在y轴上且在点N下方时,P1坐标是(0,0);
第二种情况:当P2在x轴且在M点的左侧时,P2坐标是(0,0);
第三种情况:当P3在x轴且在M点右侧时,P3坐标是(6,0);
第四种情况:当P4在y轴且在点N上方时,P4的坐标是(0,8),
综上,P坐标是(0,0)(6,0)(0,8).
点评:本题主要考查一次函数的应用,能够根据题意中的等量关系建立函数关系式;能够根据函数解析式求得对应的x的值.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
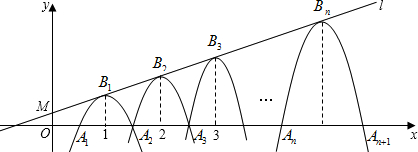

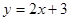 与x轴相交于点
与x轴相交于点 ,与y轴相交于点
,与y轴相交于点 .
. 与
与 轴相交于
轴相交于 ,且使
,且使 ,求
,求 的面积.
的面积.
 与x轴相交于点
与x轴相交于点 ,与y轴相交于点
,与y轴相交于点 .
. 与
与 轴相交于
轴相交于 ,且使
,且使 ,求
,求 的面积.
的面积.