题目内容
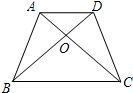20、如图，在等腰梯形ABCD中，AD∥BC，AB≠AD，对角线AC，BD相交于点O．如下四个结论：①梯形ABCD是轴对称图形；
②∠DAC=∠DCA；
③△AOB全等于△DOC；
④△AOD相似于△BOC．请把其中正确结论的序号填在横线上：
134
．分析：根据等腰梯形的性质对各个结论进行分析从而得出正确的结论．
解答：解：等腰梯形是轴对称图形，故①正确；
可证明△ABC≌△DCB∴∠BAC=∠CDB∵∠AOB=∠DOC，AB=CD∴△AOB≌△DOC，故③正确；
∵AD∥BC∴△AOD∽△BOC；
故正确的是①③④．
可证明△ABC≌△DCB∴∠BAC=∠CDB∵∠AOB=∠DOC，AB=CD∴△AOB≌△DOC，故③正确；
∵AD∥BC∴△AOD∽△BOC；
故正确的是①③④．
点评：此题综合性较强，综合考查了等腰梯形的性质、全等三角形的判定、相似三角线的判定等知识点．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在，求出这样的t的值；若不存在，请说明理由．
10、如图，在等腰梯形ABCD中，AD∥BC，AB=DC，E为AD的中点，求证：BE=CE．
已知：如图，在等腰梯形ABCD中，AD∥BC，AB=DC，点E、F分别在AB、DC上，且BE=3EA，CF=3FD．
（2012•广州）如图，在等腰梯形ABCD中，BC∥AD，AD=5，DC=4，DE∥AB交BC于点E，且EC=3，则梯形ABCD的周长是（ ）
