题目内容
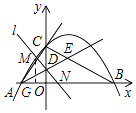
【题目】如图,已知抛物线y=ax2﹣2 ![]() ax﹣9a与坐标轴交于A,B,C三点,其中C(0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D的直线l与射线AC,AB分别交于点M,N.
ax﹣9a与坐标轴交于A,B,C三点,其中C(0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D的直线l与射线AC,AB分别交于点M,N.
(1)直接写出a的值、点A的坐标及抛物线的对称轴;
(2)点P为抛物线的对称轴上一动点,若△PAD为等腰三角形,求出点P的坐标;
(3)证明:当直线l绕点D旋转时, ![]() +
+ ![]() 均为定值,并求出该定值.
均为定值,并求出该定值.
【答案】
(1)
解:∵C(0,3).
∴﹣9a=3,解得:a=﹣ ![]() .
.
令y=0得:ax2﹣2 x﹣9a=0,
∵a≠0,
∴x2﹣2 x﹣9=0,解得:x=﹣ ![]() 或x=3
或x=3 ![]() .
.
∴点A的坐标为(﹣ ![]() ,0),B(3
,0),B(3 ![]() ,0).
,0).
∴抛物线的对称轴为x= ![]()
(2)
解:∵OA= ![]() ,OC=3,
,OC=3,
∴tan∠CAO= ![]() ,
,
∴∠CAO=60°.
∵AE为∠BAC的平分线,
∴∠DAO=30°.
∴DO= ![]() AO=1.
AO=1.
∴点D的坐标为(0,1)
设点P的坐标为( ![]() ,a).
,a).
依据两点间的距离公式可知:AD2=4,AP2=12+a2,DP2=3+(a﹣1)2.
当AD=PA时,4=12+a2,方程无解.
当AD=DP时,4=3+(a﹣1)2,解得a=2或a=0,
∴点P的坐标为( ![]() ,2)或(
,2)或( ![]() ,0).
,0).
当AP=DP时,12+a2=3+(a﹣1)2,解得a=﹣4.
∴点P的坐标为( ![]() ,﹣4).
,﹣4).
综上所述,点P的坐标为( ![]() ,2)或(
,2)或( ![]() ,0)或(
,0)或( ![]() ,﹣4)
,﹣4)
(3)
解:设直线AC的解析式为y=mx+3,将点A的坐标代入得:﹣ ![]() m+3=0,解得:m=
m+3=0,解得:m= ![]() ,
,
∴直线AC的解析式为y= ![]() x+3.
x+3.
设直线MN的解析式为y=kx+1.
把y=0代入y=kx+1得:kx+1=0,解得:x=﹣ ![]() ,
,
∴点N的坐标为(﹣ ![]() ,0).
,0).
∴AN=﹣ ![]() +
+ ![]() =
= ![]() .
.
将y= ![]() x+3与y=kx+1联立解得:x=
x+3与y=kx+1联立解得:x= ![]() .
.
∴点M的横坐标为 ![]() .
.
过点M作MG⊥x轴,垂足为G.则AG= ![]() +
+ ![]() .
.
∵∠MAG=60°,∠AGM=90°,
∴AM=2AG= ![]() +2
+2 ![]() =
= ![]() .
.
∴ ![]() +
+ ![]() =
= ![]() +
+ ![]() =
= ![]() +
+ ![]() =
= ![]() =
= ![]() =
= ![]()
【解析】(1)由点C的坐标为(0,3),可知﹣9a=3,故此可求得a的值,然后令y=0得到关于x的方程,解关于x的方程可得到点A和点B的坐标,最后利用抛物线的对称性可确定出抛物线的对称轴;(2)利用特殊锐角三角函数值可求得∠CAO=60°,依据AE为∠BAC的角平分线可求得∠DAO=30°,然后利用特殊锐角三角函数值可求得OD=1,则可得到点D的坐标.设点P的坐标为( ![]() ,a).依据两点的距离公式可求得AD、AP、DP的长,然后分为AD=PA、AD=DP、AP=DP三种情况列方程求解即可;(3)设直线MN的解析式为y=kx+1,接下来求得点M和点N的横坐标,于是可得到AN的长,然后利用特殊锐角三角函数值可求得AM的长,最后将AM和AN的长代入化简即可.
,a).依据两点的距离公式可求得AD、AP、DP的长,然后分为AD=PA、AD=DP、AP=DP三种情况列方程求解即可;(3)设直线MN的解析式为y=kx+1,接下来求得点M和点N的横坐标,于是可得到AN的长,然后利用特殊锐角三角函数值可求得AM的长,最后将AM和AN的长代入化简即可.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小,以及对特殊角的三角函数值的理解,了解分母口诀:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口诀:“123,321,三九二十七”.

【题目】“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场.顺风车行经营的A型车2015年6月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的A型车数量相同,则今年6月份A型车销售总额将比去年6月份销售总额增加25%.
(1)求今年6月份A型车每辆销售价多少元(用列方程的方法解答);
(2)该车行计划7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多? A、B两种型号车的进货和销售价格如表:
A型车 | B型车 | |
进货价格(元/辆) | 1100 | 1400 |
销售价格(元/辆) | 今年的销售价格 | 2400 |