题目内容
如图所示,△ABC∽△BEF,相似比为2:3,在△BEF中∠E=60°,EF=6,则AD的长为( )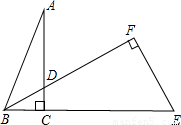
A.
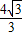
B.8
C.
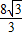
D.6
【答案】分析:先根据Rt△BEF中∠E=60°,EF=6求出BF的值,再根据△ABC∽△BEF,相似比为2:3求出AC及BC的值,由锐角三角函数的定义即可求出CD的值,进而得出AD的长.
解答:解:∵Rt△BEF中∠E=60°,EF=6,
∴∠DBC=30°,
∴BF= =
=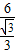 =6
=6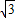 ,
,
∵△ABC∽△BEF,相似比为2:3,
∴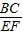 =
= ,即BC=
,即BC=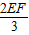 =
= =4,
=4,
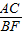 =
= ,即AC=
,即AC=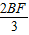 =
=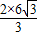 =4
=4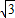 ,
,
在Rt△BCD中,
∵∠DBC=30°,BC=4,
∴CD=BC•tan30°=4×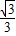 =
=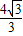 ,
,
∴AD=AC-CD=4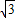 -
-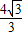 =
=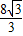 .
.
故选C.
点评:本题考查的是相似三角形的判定与性质及直角三角形的性质,熟知相似三角形对应边的比等于相似比是解答此题的关键.
解答:解:∵Rt△BEF中∠E=60°,EF=6,
∴∠DBC=30°,
∴BF=
 =
=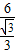 =6
=6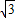 ,
,∵△ABC∽△BEF,相似比为2:3,
∴
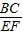 =
= ,即BC=
,即BC=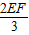 =
= =4,
=4,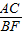 =
= ,即AC=
,即AC=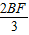 =
=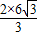 =4
=4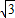 ,
,在Rt△BCD中,
∵∠DBC=30°,BC=4,
∴CD=BC•tan30°=4×
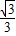 =
=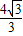 ,
,∴AD=AC-CD=4
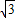 -
-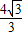 =
=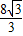 .
.故选C.
点评:本题考查的是相似三角形的判定与性质及直角三角形的性质,熟知相似三角形对应边的比等于相似比是解答此题的关键.

练习册系列答案
相关题目
 25、如图所示,△ABC和△ADE都是等边三角形,且B、A、E在同一直线上,连接BD交AC于M,连接CE交AD于N,连接MN.
25、如图所示,△ABC和△ADE都是等边三角形,且B、A、E在同一直线上,连接BD交AC于M,连接CE交AD于N,连接MN.
 34、已知如图所示,△ABC与△A′B′C′关于原点O对称,点A(-2,3),B(-4,2),C′(1,-1),则A′点的坐标为
34、已知如图所示,△ABC与△A′B′C′关于原点O对称,点A(-2,3),B(-4,2),C′(1,-1),则A′点的坐标为 如图所示,△ABC的周长为12,它的内切圆⊙O的半径为1,若向△ABC的内部随机地抛掷黄豆,则黄豆落入圆内的概率是
如图所示,△ABC的周长为12,它的内切圆⊙O的半径为1,若向△ABC的内部随机地抛掷黄豆,则黄豆落入圆内的概率是 已知如图所示,△ABC和△ABC外的一点A′,把△ABC平移,使A与A′重合.
已知如图所示,△ABC和△ABC外的一点A′,把△ABC平移,使A与A′重合.