题目内容
已知a=3,且(4tan 45°-b)2+ =0,以a,b,c为边组成的三角形面积等于( )
=0,以a,b,c为边组成的三角形面积等于( )A.6
B.7
C.8
D.9
【答案】分析:先根据非负数的性质及特殊教的三角函数值求出c,b的值,再根据三角形的三边关系判断出其形状,从而求解面积.
解答:解:∵(4tan45°-b)2+ =0,
=0,
∴4tan45°-b=0,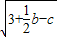 =0,
=0,
∴b=4,3+ b-c=0,∴c=5.
b-c=0,∴c=5.
又∵a2+b2=9+16=25=c2,
∴△ABC是直角三角形,且a,b为两条直角边,
∴△ABC的面积= ab=
ab= ×3×4=6.
×3×4=6.
故选A.
点评:本题考查了:①特殊角的三角函数值;②非负数的性质;③勾股定理的逆定理.
解答:解:∵(4tan45°-b)2+
 =0,
=0,∴4tan45°-b=0,
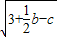 =0,
=0,∴b=4,3+
 b-c=0,∴c=5.
b-c=0,∴c=5.又∵a2+b2=9+16=25=c2,
∴△ABC是直角三角形,且a,b为两条直角边,
∴△ABC的面积=
 ab=
ab= ×3×4=6.
×3×4=6.故选A.
点评:本题考查了:①特殊角的三角函数值;②非负数的性质;③勾股定理的逆定理.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
已知a=3,且(4tan 45°-b)2+
=0,以a,b,c为边组成的三角形面积等于( )
3+
|
| A、6 | B、7 | C、8 | D、9 |
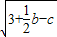 =0,以a,b,c为边组成的三角形面积等于( )
=0,以a,b,c为边组成的三角形面积等于( )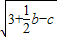 =0,以a,b,c为边组成的三角形面积等于( )
=0,以a,b,c为边组成的三角形面积等于( )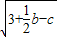 =0,以a,b,c为边组成的三角形面积等于( )
=0,以a,b,c为边组成的三角形面积等于( ) =0,以a,b,c为边组成的三角形面积等于( )
=0,以a,b,c为边组成的三角形面积等于( )