题目内容
【题目】如图,在平面直角坐标系中,△ABC的两个顶点A,B的坐标分别为(﹣2,0),(﹣1,0),BC⊥x轴,将△ABC以y轴为对称轴作轴对称变换,得到△A′B′C′(A和A′,B和B′,C和C′分别是对应顶点),直线y=x+b经过点A,C′,则点C′的坐标是 . 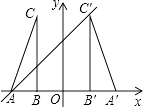
【答案】(1,3)
【解析】解:∵A(﹣2,0),B(﹣1,0), ∴AO=2,OB=1,
∵△A′B′C′和△ABC关于y轴对称,
∴OB=OB′=1,
∴B′(1,y)
∵直线y=x+b经过点A,C′,
∴ ![]() ,
,
∴点C′的坐标为(1,3).
所以答案是:(1,3).
【考点精析】本题主要考查了坐标与图形变化-对称的相关知识点,需要掌握关于x轴对称的点的特征:两个点关于x轴对称时,它们的坐标中,x相等,y的符号相反,即点P(x,y)关于x轴的对称点为P’(x,-y);关于y轴对称的点的特征:两个点关于y轴对称时,它们的坐标中,y相等,x的符号相反,即点P(x,y)关于y轴的对称点为P’(-x,y)才能正确解答此题.

练习册系列答案
相关题目