题目内容
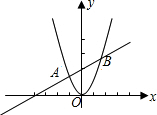 如图,一次函数y1=kx+b的图象与二次函数y2=ax2的图象交于A(-1,1.5)和B(2,6)两点,则当y1>y2时,x的取值范围是
如图,一次函数y1=kx+b的图象与二次函数y2=ax2的图象交于A(-1,1.5)和B(2,6)两点,则当y1>y2时,x的取值范围是
- A.x<-1
- B.x>2
- C.-1<x<2
- D.x<-1或x>2
C
分析:关键是从图象上找出两函数图象交点坐标,再根据两函数图象的上下位置关系,判断y1>y2时,x的范围.
解答:已知函数图象的两个交点坐标分别为(-1,1.5),(2,6),
∴当有y1>y2时,有-1<x<2.故选C.
点评:此外此题还可用数形结合的思想进行解答,由图形可以看出当y1>y2时,x的取值范围正好在A(-1,1.5)和B(2,6)两点之间,即-1<x<2.
分析:关键是从图象上找出两函数图象交点坐标,再根据两函数图象的上下位置关系,判断y1>y2时,x的范围.
解答:已知函数图象的两个交点坐标分别为(-1,1.5),(2,6),
∴当有y1>y2时,有-1<x<2.故选C.
点评:此外此题还可用数形结合的思想进行解答,由图形可以看出当y1>y2时,x的取值范围正好在A(-1,1.5)和B(2,6)两点之间,即-1<x<2.

练习册系列答案
相关题目
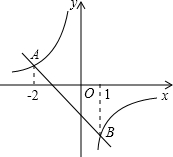 如图,一次函数y1=kx+b的图象与反比例函数y2=
如图,一次函数y1=kx+b的图象与反比例函数y2=| m |
| x |
| A、-2<x<1 |
| B、0<x<1 |
| C、x<-2和0<x<1 |
| D、-2<x<1和x>1 |
 已知:如图,一次函数y1=kx+b(k≠0)的图象与反比例函数
已知:如图,一次函数y1=kx+b(k≠0)的图象与反比例函数 如图,一次函数y1=kx+b的图象与反比例函数
如图,一次函数y1=kx+b的图象与反比例函数 如图,一次函数y1=kx+1(k≠0)与反比例函数
如图,一次函数y1=kx+1(k≠0)与反比例函数 如图,一次函数y1=kx+b与反比例函数y2=-
如图,一次函数y1=kx+b与反比例函数y2=-