题目内容
【题目】已知点P,Q为平面直角坐标系xOy中不重合的两点,以点P为圆心且经过点Q作⊙P,则称点Q为⊙P的“关联点”,⊙P为点Q的“关联圆”.
(1)已知⊙O的半径为1,在点E(1,1),F(﹣![]() ,
,![]() ),M(0,-1)中,⊙O的“关联点”为______;
),M(0,-1)中,⊙O的“关联点”为______;
(2)若点P(2,0),点Q(3,n),⊙Q为点P的“关联圆”,且⊙Q的半径为![]() ,求n的值;
,求n的值;
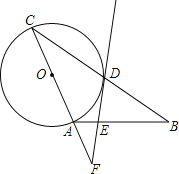
(3)已知点D(0,2),点H(m,2),⊙D是点H的“关联圆”,直线y=﹣![]() x+4与x轴,y轴分别交于点A,B.若线段AB上存在⊙D的“关联点”,求m的取值范围.
x+4与x轴,y轴分别交于点A,B.若线段AB上存在⊙D的“关联点”,求m的取值范围.
【答案】(1)F,M;(2)n=2或﹣2;(3)![]() ≤m≤
≤m≤![]() 或
或![]() ≤m≤
≤m≤![]() .
.
【解析】
(1)根据定义,认真审题即可解题,
(2)在直角三角形PHQ中勾股定理解题即可,
(3)当⊙D与线段AB相切于点T时,由sin∠OBA=![]() ,得DT=DH1=
,得DT=DH1=![]() ,进而求出m1=
,进而求出m1=![]() 即可,②当⊙D过点A时,连接AD.由勾股定理得DA=
即可,②当⊙D过点A时,连接AD.由勾股定理得DA=![]() =DH2=
=DH2=![]() 即可解题.
即可解题.
解:(1)∵OF=OM=1,
∴点F、点M在⊙上,
∴F、M是⊙O的“关联点”,
故答案为F,M.
(2)如图1,过点Q作QH⊥x轴于H.

∵PH=1,QH=n,PQ=![]() .
.
∴由勾股定理得,PH2+QH2=PQ2,
即12+n2=(![]() )2,
)2,
解得,n=2或﹣2.
(3)由y=﹣![]() x+4,知A(3,0),B(0,4)
x+4,知A(3,0),B(0,4)
∴可得AB=5
①如图2(1),当⊙D与线段AB相切于点T时,连接DT.

则DT⊥AB,∠DTB=90°
∵sin∠OBA=![]() ,
,
∴可得DT=DH1=![]() ,
,
∴m1=![]() ,
,
②如图2(2),当⊙D过点A时,连接AD.
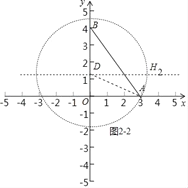
由勾股定理得DA=![]() =DH2=
=DH2=![]() .
.
综合①②可得:![]() ≤m≤
≤m≤![]() 或
或![]() ≤m≤
≤m≤![]() .
.

【题目】某校九年级(8)课外活动设置了如图所示的翻牌游戏,每次抽奖翻开一个数字,考虑“第一个人中奖排球”的机会.
正面
1 | 2 | 3 |
4 | 5 | 6 |
7 | 8 | 9 |
反面
排球 | 钢笔 | 图书 |
铅笔 | 空门 | 书包 |
球拍 | 小刀 | 篮球 |
(1)如果用实验进行估计,但制作翻奖牌没有材料,那么你有什么简便的模拟实验方法?
(2)如果不做实验,你能估计“第一个人中奖排球”的机会是多少?