题目内容
抛物线
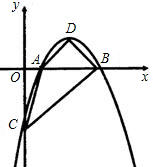
，（1）设此抛物线与x轴交点为A、B（A在B的左边），请你求出A、B两点的坐标；
（2）有一条直线y=x-1，试利用图象法求出该直线与抛物线的交点坐标；
（3）P是抛物线上的一个动点，问是否存在一点P，使S△ABP=4，若存在，则有几个这样的点P，并写出它们的坐标．
【答案】分析：（1）令抛物线解析式的y值为0，求出与x轴的交点坐标，
（2）首先找出抛物线的顶点坐标和对称轴，作出抛物线的图象，然后再作出直线的图象，解出交点坐标，
（3）假如存在P点，列出面积表达式，求出P点坐标．
解答：解：（1）令抛物线
=0，
解得x=-3或1，
故A（-3，0），B（1.0）（2分）
（2）画出图（4分），
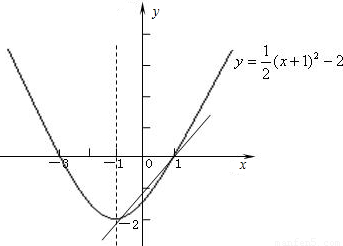
交点坐标为（1，0）和（-1，-2）（6分）
（3）存在
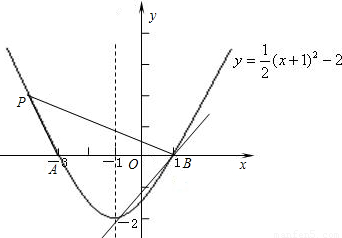
∵AB=4，S△ABP=
AB•|y|=4，
解得y=±2，
当y=2，x=±2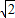
-1，
当y=-2时x=-1，
故P（2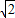
-1，2），
P（-2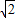
-1，2），
P（-1，-2）．（10分）
点评：本题主要考查二次函数的应用，考查二次函数与坐标轴的交点问题，不是很难．
（2）首先找出抛物线的顶点坐标和对称轴，作出抛物线的图象，然后再作出直线的图象，解出交点坐标，
（3）假如存在P点，列出面积表达式，求出P点坐标．
解答：解：（1）令抛物线
=0，解得x=-3或1，
故A（-3，0），B（1.0）（2分）
（2）画出图（4分），
交点坐标为（1，0）和（-1，-2）（6分）
（3）存在
∵AB=4，S△ABP=
AB•|y|=4，解得y=±2，
当y=2，x=±2
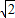-1，当y=-2时x=-1，
故P（2
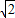-1，2），P（-2
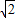-1，2），P（-1，-2）．（10分）
点评：本题主要考查二次函数的应用，考查二次函数与坐标轴的交点问题，不是很难．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
，
，
，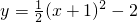