题目内容
已知抛物线y=-x2+bx+c与X轴的两个交点分别为A(m,0),B(n,0),且m+n=4,| m |
| n |
| 1 |
| 3 |
(1)求此抛物线的解析式;
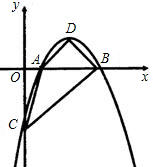
(2)设此抛物线的顶点为D,与y轴的交点为C,试判断四边形ACBD是怎样的特殊四边形,并证明你的结论.
分析:(1)根据m+n=4,
=
.就可以求出m,n的值,即得到A,B的坐标,根据待定系数法就可以求出抛物线的解析式.
(2)已知抛物线的解析式,则利用配方法就可以求出顶点D的坐标,以及与y轴的交点的坐标,利用点的坐标可分别求出∠DBA=∠DAB=∠ABC=45°.即可判断四边形的形状.
| m |
| n |
| 1 |
| 3 |
(2)已知抛物线的解析式,则利用配方法就可以求出顶点D的坐标,以及与y轴的交点的坐标,利用点的坐标可分别求出∠DBA=∠DAB=∠ABC=45°.即可判断四边形的形状.
解答:解:(1)由解得m=1,n=3,
将A(1,0),B(3,0)的坐标分别代入y=-x2+bx+c,
解得b=4,c=-3,
∴此抛物线的解析式为y=-x2+4x-3.
(2)四边形ABCD是直角梯形.
证明:∵抛物线y=-x2+4x-3与y轴交点坐标为(0,-3).
∴OC=OB,
又∵∠BOC=90°,
∴∠OCB=∠OBC=45°,
过点D作y轴的平行线交x轴于点E,
∵y=-x2+4x-3=-(x-2)2+1,
∴顶点D的坐标为(2,1),
DE⊥AB,AE=EB=DE=1,
∴∠DAE=∠DBA=45°,∠ADB=90°,
∴∠DAB=∠OBC=45°,
即AD∥BC,
又∵∠BAC>90°,∠ABD=45°,
∴AC与BD不平行.
∴四边形ABCD是直角梯形.
将A(1,0),B(3,0)的坐标分别代入y=-x2+bx+c,
解得b=4,c=-3,
∴此抛物线的解析式为y=-x2+4x-3.
(2)四边形ABCD是直角梯形.
证明:∵抛物线y=-x2+4x-3与y轴交点坐标为(0,-3).
∴OC=OB,
又∵∠BOC=90°,
∴∠OCB=∠OBC=45°,
过点D作y轴的平行线交x轴于点E,
∵y=-x2+4x-3=-(x-2)2+1,
∴顶点D的坐标为(2,1),
DE⊥AB,AE=EB=DE=1,
∴∠DAE=∠DBA=45°,∠ADB=90°,
∴∠DAB=∠OBC=45°,
即AD∥BC,
又∵∠BAC>90°,∠ABD=45°,
∴AC与BD不平行.
∴四边形ABCD是直角梯形.
点评:本题主要考查了待定系数法求函数的解析式,以及等腰直角三角形三边的关系和梯形的定义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知抛物线y=x2-8x+c的顶点在x轴上,则c等于( )
| A、4 | B、8 | C、-4 | D、16 |
 (1)求b+c的值;
(1)求b+c的值; (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.