题目内容
(2004•内江)如图,已知抛物线y=ax2+bx+c与x轴交于A(k,0)(k<0)、B(3,0)两点,与y轴正半轴交于C点,且tan∠CAO=3.(1)求此抛物线的解析式(系数中可含字母k);
(2)设点D(0,t)在x轴下方,点E在抛物线上,若四边形ADEC为平行四边形,试求t与k的函数关系式;
(3)若题(2)中的平行四边形ADEC为矩形,试求出D的坐标.

【答案】分析:(1)根据A的坐标,可得出OA的长,根据∠CAO的正切值可求出OC的长,也就能求出C点的坐标.然后根据A、B、C三点的坐标,用待定系数法求出抛物线的解析式;
(2)要想使四边形ADEC为平行四边形,AC与DE必须平行且相等.根据∠CAO的正切值可得出直线AC的斜率.也就得出了直线DE的斜率,联立直线DE和抛物线的解析式求出E点的坐标.由于AC=DE,可用E点的坐标求出DE的长,进而得出t,k的函数关系式;
(3)由于四边形ADEC为矩形,那么AD⊥AC,即直线AC与直线AD的斜率的积为-1.由此可得出t与k的函数关系式.联立(2)的关系式即可得出关于t,k的方程.可求出此时t,k的值.
解答:解:(1)∵tan∠CAO=3,A(k,0)
(k<0),又C点在y轴正半轴上
∴C(0,-3k)
∵A(k,o),B(3,0),C(0,-3k)都在抛物线上
∴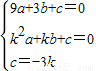
∴解得: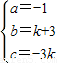
∴抛物线为:y=-x2+(k+3)x-3k;
(2)∵DE∥AC,tan∠CAO=3
∴直线DE的斜率为:3,又过点D(0,t)
∴直线DE为:y=3x+t
∴联解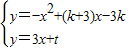 .
.
可得交点为E(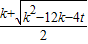 ,
,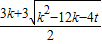 +t)
+t)
又∵要使ADEC为平行四边形
∴DE=AC
∴(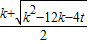 )2+(
)2+(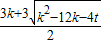 +t)2=(
+t)2=(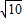 k)2
k)2
∵k<0
∴t=-2k2-3k(k<0);
(3)∵要使平行四边形ADEC为矩形
∴∠ADE=90°.
∴kAC•kAD=-1.
即:3×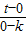 =-1,
=-1,
∴k=3t.
又∵t=-2k2-3k
∴由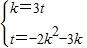 .
.
得t=- 或t=0(舍)
或t=0(舍)
∴D点的坐标为(0,- ).
).
点评:本题着重考查了待定系数法求二次函数解析式、解直角三角形、平行四边形的判定、矩形的判定和性质等知识点,(2)、(3)中利用好一次函数平行和垂直时斜率的关系是解题的关键.要牢记一次函数的斜率公式:k=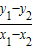 .
.
(2)要想使四边形ADEC为平行四边形,AC与DE必须平行且相等.根据∠CAO的正切值可得出直线AC的斜率.也就得出了直线DE的斜率,联立直线DE和抛物线的解析式求出E点的坐标.由于AC=DE,可用E点的坐标求出DE的长,进而得出t,k的函数关系式;
(3)由于四边形ADEC为矩形,那么AD⊥AC,即直线AC与直线AD的斜率的积为-1.由此可得出t与k的函数关系式.联立(2)的关系式即可得出关于t,k的方程.可求出此时t,k的值.
解答:解:(1)∵tan∠CAO=3,A(k,0)
(k<0),又C点在y轴正半轴上
∴C(0,-3k)
∵A(k,o),B(3,0),C(0,-3k)都在抛物线上
∴
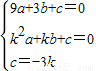
∴解得:
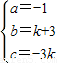
∴抛物线为:y=-x2+(k+3)x-3k;
(2)∵DE∥AC,tan∠CAO=3
∴直线DE的斜率为:3,又过点D(0,t)
∴直线DE为:y=3x+t
∴联解
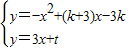 .
.可得交点为E(
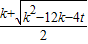 ,
,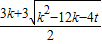 +t)
+t)又∵要使ADEC为平行四边形
∴DE=AC
∴(
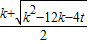 )2+(
)2+(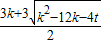 +t)2=(
+t)2=(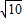 k)2
k)2∵k<0
∴t=-2k2-3k(k<0);
(3)∵要使平行四边形ADEC为矩形
∴∠ADE=90°.
∴kAC•kAD=-1.
即:3×
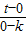 =-1,
=-1,∴k=3t.
又∵t=-2k2-3k
∴由
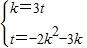 .
.得t=-
 或t=0(舍)
或t=0(舍)∴D点的坐标为(0,-
 ).
).点评:本题着重考查了待定系数法求二次函数解析式、解直角三角形、平行四边形的判定、矩形的判定和性质等知识点,(2)、(3)中利用好一次函数平行和垂直时斜率的关系是解题的关键.要牢记一次函数的斜率公式:k=
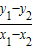 .
. 
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目

 ?如果存在,则求出求出对应的x值;如果不存在,则说明理由.
?如果存在,则求出求出对应的x值;如果不存在,则说明理由.

 ?如果存在,则求出求出对应的x值;如果不存在,则说明理由.
?如果存在,则求出求出对应的x值;如果不存在,则说明理由.