题目内容
(2004•内江)如图,等腰直角三角形ABC的斜边BC的长为8,平行于BC边的直线分别交AB,AC于M,N,将△AMN沿直线MN翻折,得到△A′MN,设△A′MN与△ABC的公共部分的面积为y,MN的长为x.(1)如果A′在△ABC的内部,求出以x为自变量的函数y的解析式,并指出自变量x的取值范围;
(2)是否存在直线MN,使y的值为△ABC面积的
 ?如果存在,则求出求出对应的x值;如果不存在,则说明理由.
?如果存在,则求出求出对应的x值;如果不存在,则说明理由.
【答案】分析:(1)根据等腰直角三角形斜边上的高也是斜边上的中线,则等于斜边的一半.再根据三角形的面积公式进行计算,要求自变量的取值范围,根据A′在△ABC的内部和轴对称的性质则x的值应小于斜边的一半;
(2)如果是(1)中的情况,根据相似三角形的面积比是相似比的平方,则y的值一定小于△ABC面积的 .所以应考虑点A′在三角形的外部的情况.表示出y的解析式,再列方程求解即可.
.所以应考虑点A′在三角形的外部的情况.表示出y的解析式,再列方程求解即可.
解答:解:(1)连接AA′,交MN于D,则:由对称性知AA′⊥BC,AD=A′D
又∵MN∥BC
∴AB=AC
∴AA′⊥BC(设与BC交于D′或延长线交于D′)
又∵MN∥BC
∴∠AMD=45°
∴AD=MD= MN=
MN= x
x
∴y= x2
x2
又∵要使A′在△ABC内部
∴AA′<AD′= BC=4
BC=4
∴AD< AA′=2
AA′=2
故:MN=x<2AD=4
于是:y= x2(x<4);
x2(x<4);
(2)要使y的值为△ABC面积的 ,则点A′一定在三角形的外部.
,则点A′一定在三角形的外部.
又y= x2-
x2- ×(x-4)×(2x-8)=-
×(x-4)×(2x-8)=- x2+8x-16.
x2+8x-16.
∴- x2+8x-16=
x2+8x-16= ×
× ×8×4
×8×4
解得x1=x2=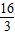
∴存在直线MN使y的值为△ABC面积的 .
.
点评:此题主要是运用了等腰三角形的性质以及三角形的面积公式,能够根据不同的情况得到不同的函数关系式.
(2)如果是(1)中的情况,根据相似三角形的面积比是相似比的平方,则y的值一定小于△ABC面积的
 .所以应考虑点A′在三角形的外部的情况.表示出y的解析式,再列方程求解即可.
.所以应考虑点A′在三角形的外部的情况.表示出y的解析式,再列方程求解即可.解答:解:(1)连接AA′,交MN于D,则:由对称性知AA′⊥BC,AD=A′D
又∵MN∥BC
∴AB=AC
∴AA′⊥BC(设与BC交于D′或延长线交于D′)
又∵MN∥BC
∴∠AMD=45°
∴AD=MD=
 MN=
MN= x
x∴y=
 x2
x2又∵要使A′在△ABC内部
∴AA′<AD′=
 BC=4
BC=4∴AD<
 AA′=2
AA′=2故:MN=x<2AD=4
于是:y=
 x2(x<4);
x2(x<4);(2)要使y的值为△ABC面积的
 ,则点A′一定在三角形的外部.
,则点A′一定在三角形的外部.又y=
 x2-
x2- ×(x-4)×(2x-8)=-
×(x-4)×(2x-8)=- x2+8x-16.
x2+8x-16.∴-
 x2+8x-16=
x2+8x-16= ×
× ×8×4
×8×4解得x1=x2=
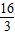
∴存在直线MN使y的值为△ABC面积的
 .
.点评:此题主要是运用了等腰三角形的性质以及三角形的面积公式,能够根据不同的情况得到不同的函数关系式.

练习册系列答案
相关题目

 ?如果存在,则求出求出对应的x值;如果不存在,则说明理由.
?如果存在,则求出求出对应的x值;如果不存在,则说明理由.

