Question

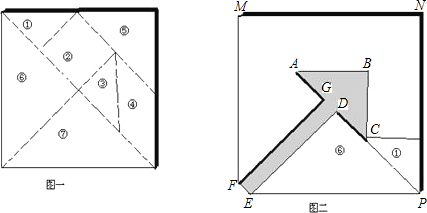
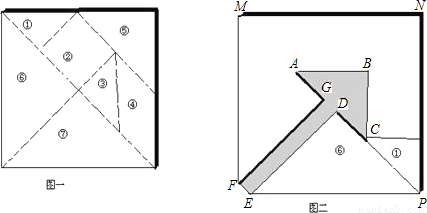
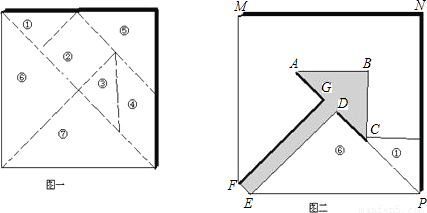
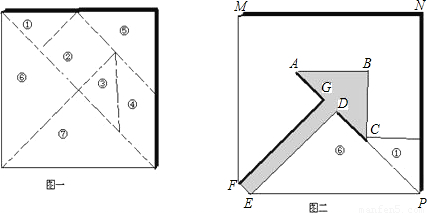
将一个正方形纸板（如图-）沿虚线剪下，得到七块几何图形的纸板（其中①③⑤⑥⑦是等腰直角三角形，②是正方形）我们把这七块纸板叫做七巧板．现用七巧板拼出一个图形，其空隙部分是一个箭头（如图二）．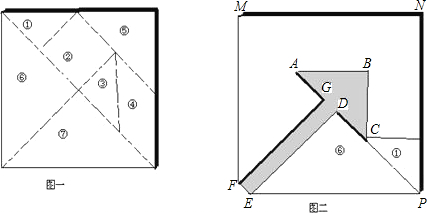

（1）请在图二中用实线画出拼图的痕迹（如实线DP）；
（2）如果图一中大正方形纸板的边长为10，计算图二中“箭头”的面积（即封闭平面图形ABCDEFG的面积）．

Answer 1

分析：根据七巧板的特性结合题意解答．

解答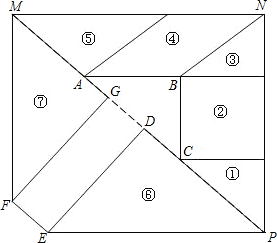：解：（1）如图：（2分）

（2）连接GD．
∵AB=BC=

5

2

2

，MN=NP=

15

2

2

，MG=DP=5

2

，
∴MP=15，
∴GD=15-10

2

，（4分）
∴S_△ABC=

1

2

×

5

2

2

×

5

2

2

=

25

4

，（5分）
S_矩形EFGD=5

2

×（15-10

2

）=75

2

-100．  （6分）
∴封闭图形ABCDEFG的面积=S_△ABC+S_矩形EFGD
=

25

4

+75

2

-100=75

2

-

375

4

．           （7分）

点评：本题通过七巧板考查常见图形的有关计算能力．