题目内容
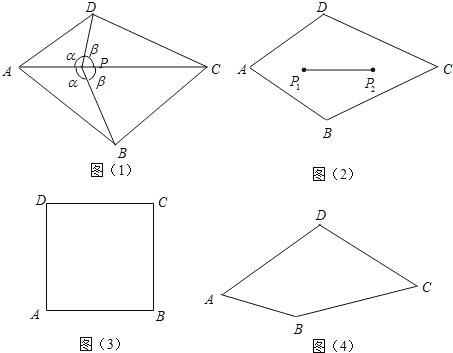
【题目】如图(1),凸四边形ABCD,如果点P满足∠APD=∠APB=α.且∠BPC=∠CPD=β,则称点P为四边形ABCD的一个半等角点.
【1】在图(3)正方形ABCD内画一个半等角点P,且满足α≠β;
【2】在图(4)四边形ABCD中画出一个半等角点P,保留画图痕迹(不需写出画法);
【3】若四边形ABCD有两个半等角点P1、P2(如图(2)),证明线段P1P2上任一点也是它的半等角点.
【答案】
【1】所画的点P在AC上且不是AC的中点和AC的端点.(2分)
【2】画点B关于AC的对称点B’,延长DB’交AC于点P,点P为所求(不写文字说明不扣分).(3分)
【3】连P1A、P1D、P1B、P1C和P2D、P2B,根据题意,
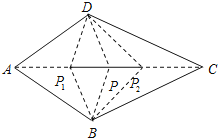
∠AP1D=∠AP1B,∠DP1C=∠BP1C,
∴∠AP1B+∠BP1C=180度.
∴P1在AC上,
同理,P2也在AC上.
在△DP1P2和△BP1P2中,
∠DP2P1=∠BP2P1,∠DP1P2=∠BP1P2,P1P2公共,
∴△DP1P2≌△BP1P2.
所以DP1=BP1,DP2=BP2,于是B、D关于AC对称.
设P是P1P2上任一点,连接PD、PB,由对称性,得∠DPA=∠BPA,∠DPC=∠BPC,
所以点P是四边形的半等角点.(5分)
【解析】(1)根据题意可知,所画的点P在AC上且不是AC的中点和AC的端点.因为在图形内部,所以不能是AC的端点,又由于α≠β,所以不是AC的中点.
(2)画点B关于AC的对称点B’,延长DB’交AC于点P,点P为所求.(因为对称的两个图形完全重合)
(3)先连P1A、P1D、P1B、P1C和P2D、P2B,根据题意∠AP1D=∠AP1B,∠DP1C=∠BP1C∴∠AP1B+∠BP1C=180度.∴P1在AC上,同理,P2也在AC上,再利用ASA证明△DP1P2≌△BP1P2而,那么△P1DP2和△P1BP2关于P1P2对称,P是对称轴上的点,所以∠DPA=∠BPA,∠DPC=∠BPC.即点P是四边形的半等角点

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案