题目内容
【题目】已知a、b、c为整数，且满足3+a2+b2+c2＜ab+3b+2c，求
的值．
【答案】解：由a、b、c均为整数，a2+b2+c2+3＜ab+3b+2c，得
a2+b2+c2+3≤ab+3b+2c﹣1
∴4a2+4b2+4c2+12≤4ab+12b+8c﹣4
（4a2﹣4ab+b2）+（3b2﹣12b+12）+（4c2﹣8c+4）≤0
（2a﹣b）2+3（b2﹣4b+4）+4（c2﹣2c+1）≤0
（2a﹣b）2+3（b﹣2）2+4（c﹣1）2≤0
∴2a﹣b=0，b﹣2=0，c﹣1=0，
解得 a=1，b=2，c=1，
∴
=
．
【解析】由a、b、c为整数，可得应把所给不等式的右边减1，整理为用“≤”表示的形式，进而把得到的不等式整理为一边为0的形式，把另一边整理3个不含分数的完全平方式子的和的形式，让底数为0可得a，b，c的值，进而代入代数式求解即可．
【考点精析】关于本题考查的根与系数的关系，需要了解一元二次方程ax2+bx+c=0（a≠0）的根由方程的系数a、b、c而定；两根之和等于方程的一次项系数除以二次项系数所得的商的相反数；两根之积等于常数项除以二次项系数所得的商才能得出正确答案．
导学教程高中新课标系列答案
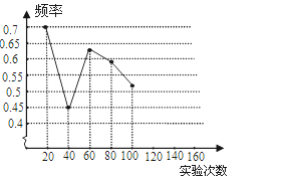
小学课时特训系列答案
【题目】一粒木质中国象棋棋子“車”，它的正面雕刻一个“車”字，它的反面是平的，将棋子从一定高度下抛，落地反弹后可能是“車”字面朝上，也可能是“車”字朝下．由于棋子的两面不均匀，为了估计“車”字朝上的机会，某实验小组做了棋子下抛实验，并把实验数据整理如下：
实验次数 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
“車”字朝上的频数 | 14 | 18 | 38 | 47 | 52 |
| 78 | 88 |
相应的频率 | 0.7 | 0.45 | 0.63 | 0.59 | 0.52 | 0.55 | 0.56 |
|
（1）请将表中数据补充完整，并画出折线统计图中剩余部分．
（2）如果实验继续进行下去，根据上表数据，这个实验的频率将接近于该事件发生的机会，请估计这个机会约是多少？
（3）在（2）的基础上，进一步估计：将该“車”字棋子，按照实验要求连续抛2次，则刚好使“車”字一次字面朝上，一次朝下的可能性为多少？
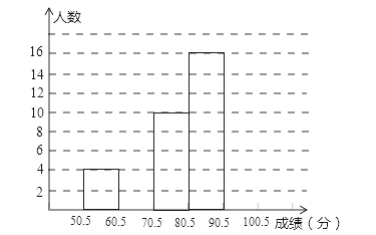
【题目】为了让学生了解环保知识，增强环保意识，某中学举行了一次“环保知识竞赛”，共有850名学生参加了这次竞赛，为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取整数，满分为100分）进行统计．请你根据尚未完成并有局部污染的频率分布表和频率分布直方图，解答下列问题：
分 组 | 频数 | 频率 |
50.5～60.5 | 4 | 0.08 |
60.5～70.5 | 0.16 | |
70.5～80.5 | 10 | |
80.5～90.5 | 16 | 0.32 |
90.5～100.5 | ||
合 计 | 50 | 1.00 |
（1）填充频率分布表的空格；
（2）补全频数直方图，并在此图上直接绘制频数分布折线图；
（3）全体参赛学生中，竞赛成绩落在哪组范围内的人数最多？
（4）若成绩在90分以上（不含90分）为优秀，则该校成绩优秀的约为多少人？
