题目内容
（2010•来宾）已知反比例函数的图象过点（-2，-2）．（1）求此反比例函数的关系式；
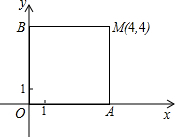
（2）过点M（4，4）分别作x、y轴的垂线，垂足分别为A、B，这两条垂线与x、y轴围成一个正方形OAMB（如图），用列表法写出在这个正方形内（包括正方形的边和内部）且位于第一象限，横、纵坐标都是整数的点的坐标；并求在这些点中任取一点，该点恰好在所求反比例函数图象上的概率P．
分析：（1）设出反比例函数的解析式，把点（-2，-2）代入解析式即可求出k的值，进而得出反比例函数的解析式；
（2）用列表法写出在这个正方形内（包括正方形的边和内部）且位于第一象限，横、纵坐标都是整数的点的坐标，根据反比例函数中k=xy的特点即可求出这些点中在反比例函数图象上的点，求出其概率即可．
（2）用列表法写出在这个正方形内（包括正方形的边和内部）且位于第一象限，横、纵坐标都是整数的点的坐标，根据反比例函数中k=xy的特点即可求出这些点中在反比例函数图象上的点，求出其概率即可．
解答：解：（1）设反比例函数的解析式为y=
（k≠0），
∵反比例函数的图象过点（-2，-2）．
∴-2=
，解得k=4，
∴反比例函数的解析式为：y=
；
（2）正方形内（包括正方形的边和内部）且位于第一象限，横、纵坐标都是整数的点的坐标如表所示：
∵1×4=4，2×2=4，4×1=4，
∴点（1，4）、（2，2）、（4，1）在反比例函数y=
的图象上，其概率P=
．
| k |
| x |
∵反比例函数的图象过点（-2，-2）．
∴-2=
| k |
| -2 |
∴反比例函数的解析式为：y=
| 4 |
| x |
（2）正方形内（包括正方形的边和内部）且位于第一象限，横、纵坐标都是整数的点的坐标如表所示：
| 纵坐标 横坐标 |
0 | 1 | 2 | 3 | 4 |
| 0 | （0，0） | （0，1） | （0，2） | （0，3） | （0，4） |
| 1 | （1，0） | （1，1） | （1，2） | （1，3） | （1，4） |
| 2 | （2，0） | （2，1） | （2，2） | （2，3） | （2，4） |
| 3 | （3，0） | （3，1） | （3，2） | （3，3） | （3，4） |
| 4 | （4，0） | （4，1） | （4，2） | （4，3） | （4，4） |
∴点（1，4）、（2，2）、（4，1）在反比例函数y=
| 4 |
| x |
| 3 |
| 25 |
点评：本题考查的是反比例函数综合题，涉及到用待定系数法求反比例函数的解析式及概率公式，难度适中．
练习册系列答案
相关题目
（2010•来宾）已知在Rt△ABC中，∠C=90°，点E在边AB上，且AE=AC，∠BAC的平分线AD与BC交于点D．
（2010•来宾）已知矩形OABC的顶点O在平面直角坐标系的原点，边OA、OC分别在x、y轴的正半轴上，且OA=3cm，OC=4cm，点M从点A出发沿AB向终点B运动，点N从点C出发沿CA向终点A运动，点M、N同时出发，且运动的速度均为1cm/秒，当其中一个点到达终点时，另一点即停止运动．设运动的时间为t秒．