题目内容
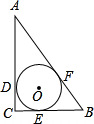 如图,已知⊙O内切于△ABC,切点分别为D、E、F,∠C=90°,⊙O的面积为4πcm2,AC=8cm,则AB=________cm.
如图,已知⊙O内切于△ABC,切点分别为D、E、F,∠C=90°,⊙O的面积为4πcm2,AC=8cm,则AB=________cm.
10
分析:设⊙O的半径为r,根据⊙O的面积,可求得r的值;连接OD、OE,易证得四边形ODCE是正方形,即CD=CE=r;在Rt△ACB中,用r表示出AD、AF、CE的长,设BF=BE=x,根据勾股定理,可列出关于x的方程,即可求出x的值,进而可求出AB的长.
解答: 解:设⊙O的半径为r,依题意,有:
解:设⊙O的半径为r,依题意,有:
πr2=4π,即r=2cm(负值舍去);
连接OD、OE;则四边形ODCE是正方形;
∴OD=CD=CE=r=2cm;
根据切线长定理,可得:AD=AF=AC-AD=6cm;
设BE=BF=x,则AB=6+x,BC=2+x;
根据勾股定理,得:64+(2+x)2=(6+x)2,
解得x=4cm,则AB=10cm.
点评:此题考查了直角三角形内切圆的性质以及内切圆半径的求法.
分析:设⊙O的半径为r,根据⊙O的面积,可求得r的值;连接OD、OE,易证得四边形ODCE是正方形,即CD=CE=r;在Rt△ACB中,用r表示出AD、AF、CE的长,设BF=BE=x,根据勾股定理,可列出关于x的方程,即可求出x的值,进而可求出AB的长.
解答:
 解:设⊙O的半径为r,依题意,有:
解:设⊙O的半径为r,依题意,有:πr2=4π,即r=2cm(负值舍去);
连接OD、OE;则四边形ODCE是正方形;
∴OD=CD=CE=r=2cm;
根据切线长定理,可得:AD=AF=AC-AD=6cm;
设BE=BF=x,则AB=6+x,BC=2+x;
根据勾股定理,得:64+(2+x)2=(6+x)2,
解得x=4cm,则AB=10cm.
点评:此题考查了直角三角形内切圆的性质以及内切圆半径的求法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
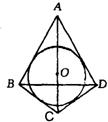 23、如图,已知⊙O内切于四边形ABCD,AB=AD,连接AC、BD,由这些条件你能推出哪些结论(不再标注其它字母,不再添加辅助线,不写推理过程)写出六条结论即可.
23、如图,已知⊙O内切于四边形ABCD,AB=AD,连接AC、BD,由这些条件你能推出哪些结论(不再标注其它字母,不再添加辅助线,不写推理过程)写出六条结论即可. 4、如图,已知⊙O内切于△ABC,切点分别为D、E、F,∠C=90°,⊙O的面积为4πcm2,AC=8cm,则AB=
4、如图,已知⊙O内切于△ABC,切点分别为D、E、F,∠C=90°,⊙O的面积为4πcm2,AC=8cm,则AB= 如图,已知⊙O内切于菱形ABCD,MN,PQ与圆O相切,M,N,P,Q分别在AB,BC,CD,DA上,求证:MQ∥PN.
如图,已知⊙O内切于菱形ABCD,MN,PQ与圆O相切,M,N,P,Q分别在AB,BC,CD,DA上,求证:MQ∥PN. 如图,已知⊙O内切于菱形ABCD,MN,PQ与圆O相切,M,N,P,Q分别在AB,BC,CD,DA上,求证:MQ∥PN.
如图,已知⊙O内切于菱形ABCD,MN,PQ与圆O相切,M,N,P,Q分别在AB,BC,CD,DA上,求证:MQ∥PN.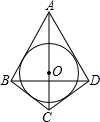 如图,已知⊙O内切于四边形ABCD,AB=AD,连接AC、BD,由这些条件你能推出哪些结论(不再标注其它字母,不再添加辅助线,不写推理过程)写出六条结论即可.
如图,已知⊙O内切于四边形ABCD,AB=AD,连接AC、BD,由这些条件你能推出哪些结论(不再标注其它字母,不再添加辅助线,不写推理过程)写出六条结论即可.