Question

如图，已知⊙O内切于菱形ABCD，MN，PQ与圆O相切，M，N，P，Q分别在AB，BC，CD，DA上，求证：MQ∥PN．

Answer 1

证明：连接AC、BD，其交点为内切圆心O．

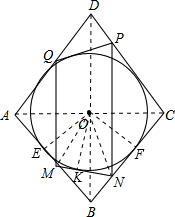
设MN与⊙O切于K，圆O与AB和BC分别交于E、F，连接OE、OM、OK、ON、OF．
记∠ABO=φ，∠MOK=α，∠KON=β，
则∠EOM=α，∠FON=β，∠EOF=2α+2β=180°-2φ．，
∴∠BON=90°-∠NOF-∠COF=90°-β-φ=α，
∴∠CNO=∠NBO+∠NOB=φ+α=∠AOE+∠MOE=∠AOM，
又∵∠OCN=∠MAO，
∴△OCN∽△MAO，
∴AM•CN=AO•CO；
同理可证得：AQ•CP=AO•CO．
继而得出AM•CN=AQ•CP，
又∵∠A=∠C，
∴△AMQ∽△CPN，
∴∠AMQ=∠CPN，
继而得出MQ∥PN．
分析：要证MQ∥NP，只需证∠AMQ=∠CPN，结合∠A=∠C知，只需证△AMQ∽△CPN，进而只需要证明AM•CN=AQ•CP即可．
点评：本题是一道竞赛题，考查菱形的性质，难度较大，同时要注意切线性质的熟练掌握与灵活运用．