题目内容
【题目】定义:若线段AB上有一点P,当PA=PB时,则称点P为线段AB的中点。
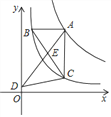
已知数轴上A,B两点对应数分别为a和b,![]() ,P为数轴上一动点,对应数为x.
,P为数轴上一动点,对应数为x.
(1)a=______,b=_______;
(2)若点P为线段AB的中点,则P点对应的数![]() 为______________.若B为线段AP的中点时则P点对应的数
为______________.若B为线段AP的中点时则P点对应的数![]() 为______________。
为______________。
(3)若点A、点B同时向左运动,它们的速度都为1个单位长度/秒,与此同时点P从-16处以2个单位长度/秒向右运动。
①设运动的时间为t秒,直接用含t的式子填空
AP=____________;BP=______________。
②经过多长时间后,点A、点B、点P三点中其中一点是另外两点的中点?

【答案】(1)-2、4;(2)1、10;(3)①-3t+14或14-3t;20-3t或3t-20;②t=![]() ,t=
,t=![]() ,t=
,t=![]() .
.
【解析】
(1)根据非负数的性质解答即可;
(2)根据线段中点的定义得出规律:若A表示的数为a,B表示的数为b,P表示的数为x,P为线段AB的中点,则2x=a+b,然后根据这个规律解答即可.
(3)①根据题意得出A、B、P表示的数,从而得出结论;
②分三种情况讨论:若P为AB的中点,若A为BP的中点,若B为AP的中点,根据(2)得出的结论列方程求解即可.
(1)根据题意得:a+2=0,b-4=0,解得:a=-2,b=4.
故答案为:-2,4.
(2)∵P为线段AB的中点,∴AP=PB,∴x-a= b-x,∴2x=a+b,∴x=![]() =
=![]() =1;
=1;
若B为线段AP的中点,则2b=a+x,解得:x=2b-a=8-(-2)=10.
故答案为:1,10.
(3)由题意得:A表示的数为:-2-t,B表示的数为:4-t,P表示的数为:-16+2t.
①AP=|(-16+2t)-(-2-t)|=|14-3t|,BP=|(-16+2t)-(4-t)|=|20-3t|,∴AP=-3t+14或14-3t;BP=20-3t或3t-20.
故答案为:-3t+14或14-3t;20-3t或3t-20.
②分三种情况讨论:
若P为AB的中点,则:2(-16+2t)=(-2-t)+(4-t),解得:t=![]() ;
;
若A为BP的中点,则:2(-2-t)=(-16+2t)+(4-t),解得:t=![]() ;
;
若B为AP的中点,则:2(4-t)=(-2-t)+(-16+2t),解得:t=![]() .
.
综上所述:t的值为![]() 或
或![]() 或
或![]() 时,点A、点B、点P三点中其中一点是另外两点的中点.
时,点A、点B、点P三点中其中一点是另外两点的中点.

【题目】观察如图图形,把一个三角形分别连接其三边中点,构成4个小三角形,挖去中间的一个小三角形(如图1),对剩下的三个小三角形再分别重复以上做法,……,据此解答下面的问题
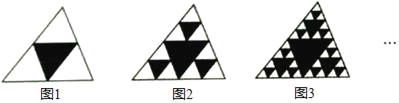
(1)填写下表:
图形 | 挖去三角形的个数 |
图形1 | 1 |
图形2 | 1+3 |
图形3 | 1+3+9 |
图形4 |
|
(2)根据这个规律,求图n中挖去三角形的个数wn;(用含n的代数式表示)
(3)若图n+1中挖去三角形的个数为wn+1,求wn+1﹣Wn