题目内容
若直线l:y=x+3交x轴于点A,交y轴于点B.坐标原点O关于直线l的对称点O′在反比例函数y=| k |
| x |
(1)求反比例函数y=
| k |
| x |
(2)将直线l绕点A逆时针旋转角θ(0°<θ<45°),得到直线l′,l′交y轴于点P,过点P作x轴的平行线,与上述反比例函数y=
| k |
| x |
3
| ||
| 2 |
分析:(1)求出点A、B的坐标,然后根据坐标原点O与O′关于直线l对称求出点O′,再利用待定系数法即可求解;
(2)根据题意作出草图,设点P的坐标为(0,a),先求出点Q的坐标,然后分别求出梯形O′BPQ的面积与正方形AOBO′的面积,再根据S四边形APQO′=S梯形O′BPQ的面积+S正方形AOBO′-S△AOP,列式计算即可求出a的值为3
,根据三角函数求出∠PAO=60°,∠BAO=45°,两角相减即可得到θ的值.
(2)根据题意作出草图,设点P的坐标为(0,a),先求出点Q的坐标,然后分别求出梯形O′BPQ的面积与正方形AOBO′的面积,再根据S四边形APQO′=S梯形O′BPQ的面积+S正方形AOBO′-S△AOP,列式计算即可求出a的值为3
| 3 |
解答: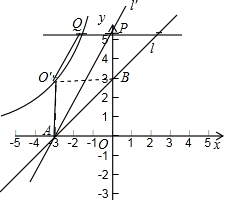 解:(1)当x=0时,y=0+3=3,
解:(1)当x=0时,y=0+3=3,
当y=0时,x+3=0,解得x=-3,
∴点A、B的坐标分别为A(-3,0),B(0,3),
∵坐标原点O与O′关于直线l对称,
∴O′(-3,3),
∴3=
,
解得k=-9,
∴反比例函数y=
的解析式为:y=-
;
(2)设点P的坐标为(0,a),
∵PQ∥x轴,
∴a=-
,
解得x=-
,
∴点Q的坐标为(-
,a);
S四边形APQO′=S梯形O′BPQ的面积+S正方形AOBO′-S△AOP=
×(
+3)(a-3)+3×3-
×3×a,
=-
+9,
∵四边形APQO′的面积为9-
,
∴-
+9=9-
,
解得a=3
,
∴tan∠PAO=
=
=
,tan∠BAO=
=
=1,
∴∠PAO=60°,∠BAO=45°,
θ=∠PAO-∠BAO=60°-45°=15°.
故答案为:15°.
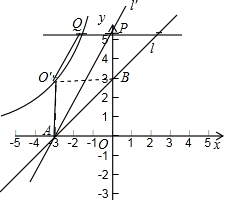 解:(1)当x=0时,y=0+3=3,
解:(1)当x=0时,y=0+3=3,当y=0时,x+3=0,解得x=-3,
∴点A、B的坐标分别为A(-3,0),B(0,3),
∵坐标原点O与O′关于直线l对称,
∴O′(-3,3),
∴3=
| k |
| -3 |
解得k=-9,
∴反比例函数y=
| k |
| x |
| 9 |
| x |
(2)设点P的坐标为(0,a),
∵PQ∥x轴,
∴a=-
| 9 |
| x |
解得x=-
| 9 |
| a |
∴点Q的坐标为(-
| 9 |
| a |
S四边形APQO′=S梯形O′BPQ的面积+S正方形AOBO′-S△AOP=
| 1 |
| 2 |
| 9 |
| a |
| 1 |
| 2 |
=-
| 27 |
| 2a |
∵四边形APQO′的面积为9-
3
| ||
| 2 |
∴-
| 27 |
| 2a |
3
| ||
| 2 |
解得a=3
| 3 |
∴tan∠PAO=
| PO |
| AO |
3
| ||
| 3 |
| 3 |
| BO |
| AO |
| 3 |
| 3 |
∴∠PAO=60°,∠BAO=45°,
θ=∠PAO-∠BAO=60°-45°=15°.
故答案为:15°.
点评:本题综合考查了反比例函数与一次函数的性质,此题难度稍大,综合性比较强,注意不规则四边形APQO′的面积的表示是解题的关键,也是解本题的难点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
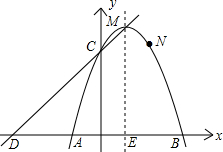 3)三点,且与y轴交于点C.
3)三点,且与y轴交于点C.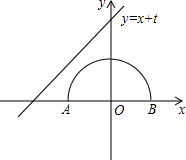 如图,半圆的圆心与坐标原点重合,圆的半径为1,直线l的解析式为y=x+t.若直线l与半圆只有一个交点,则t的取值范围是
如图,半圆的圆心与坐标原点重合,圆的半径为1,直线l的解析式为y=x+t.若直线l与半圆只有一个交点,则t的取值范围是 (2010•本溪一模)在直角坐标系中,放置一个如图的直角三角形纸片AOB,已知OA=2,∠AOB=30°,D、E两点同时从原点O出发,D点以每秒
(2010•本溪一模)在直角坐标系中,放置一个如图的直角三角形纸片AOB,已知OA=2,∠AOB=30°,D、E两点同时从原点O出发,D点以每秒 (2012•乐陵市二模)如图,在平面直角坐标系中,线段AB的端点坐标为A(-1,2),B(3,1),若直线y=kx-2与线段AB有交点,则k的值可能是( )
(2012•乐陵市二模)如图,在平面直角坐标系中,线段AB的端点坐标为A(-1,2),B(3,1),若直线y=kx-2与线段AB有交点,则k的值可能是( )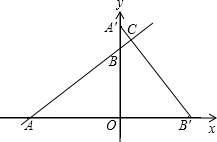 点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.