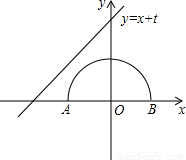题目内容
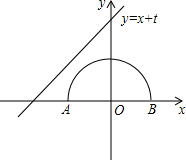 如图,半圆的圆心与坐标原点重合,圆的半径为1,直线l的解析式为y=x+t.若直线l与半圆只有一个交点,则t的取值范围是
如图,半圆的圆心与坐标原点重合,圆的半径为1,直线l的解析式为y=x+t.若直线l与半圆只有一个交点,则t的取值范围是分析:若直线与半圆只有一个交点,则有两种情况:直线和半圆相切于点C或从直线过点A开始到直线过点B结束(不包括直线过点A).
直线过点B.
当直线和半圆相切于点C时,根据直线的解析式知直线与x轴所形成的锐角是45°,从而求得DOC=45°,即可求出点C的坐标,进一步求得t的值;当直线过点B时,直接根据待定系数法求得t的值.
若直线L与半圆有交点,则直线从和半圆相切于点C开始到直线过点B结束(包括上述两种情况).
直线过点B.
当直线和半圆相切于点C时,根据直线的解析式知直线与x轴所形成的锐角是45°,从而求得DOC=45°,即可求出点C的坐标,进一步求得t的值;当直线过点B时,直接根据待定系数法求得t的值.
若直线L与半圆有交点,则直线从和半圆相切于点C开始到直线过点B结束(包括上述两种情况).
解答: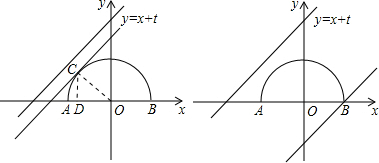
解:若直线与半圆只有一个交点,则有两种情况:直线和半圆相切于点C或从直线过点A开始到直线过点B结束(不包括直线过点A).
直线y=x+t与x轴所形成的锐角是45°.
当直线和半圆相切于点C时,则OC垂直于直线,∠COD=45°.
又OC=1,则CD=OD=
,即点C(-
,
).
把点C的坐标代入直线解析式,得
t=y-x=
;
当直线过点B时,把点A(-1,0)代入直线解析式,得t=y-x=1.
当直线过点B时,把点B(1,0)代入直线解析式,得t=y-x=-1.
即t=
或-1≤t≤1时,直线和圆只有一个公共点;
若直线和圆有公共点,则-1≤t≤
.
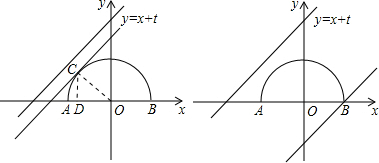
解:若直线与半圆只有一个交点,则有两种情况:直线和半圆相切于点C或从直线过点A开始到直线过点B结束(不包括直线过点A).
直线y=x+t与x轴所形成的锐角是45°.
当直线和半圆相切于点C时,则OC垂直于直线,∠COD=45°.
又OC=1,则CD=OD=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
把点C的坐标代入直线解析式,得
t=y-x=
| 2 |
当直线过点B时,把点A(-1,0)代入直线解析式,得t=y-x=1.
当直线过点B时,把点B(1,0)代入直线解析式,得t=y-x=-1.
即t=
| 2 |
若直线和圆有公共点,则-1≤t≤
| 2 |
点评:此题综合考查了直线和圆的位置关系,及用待定系数法求解直线的解析式等方法.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
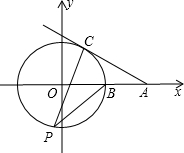 (2012•郧县三模)如图,⊙O的圆心在坐标原点,⊙O与x轴正半轴交于点B,延长OB至点A使AB=OB,过点A作⊙O的切线AC,切点为C,P为⊙O上一点(不在弧BC上),则cos∠BPC的值为( )
(2012•郧县三模)如图,⊙O的圆心在坐标原点,⊙O与x轴正半轴交于点B,延长OB至点A使AB=OB,过点A作⊙O的切线AC,切点为C,P为⊙O上一点(不在弧BC上),则cos∠BPC的值为( )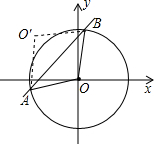 (2012•连云港)如图,⊙O的圆心在坐标原点,半径为2,直线y=x+b(b>0)与⊙O交于A、B两点,点O关于直线y=x+b的对称点O′,
(2012•连云港)如图,⊙O的圆心在坐标原点,半径为2,直线y=x+b(b>0)与⊙O交于A、B两点,点O关于直线y=x+b的对称点O′,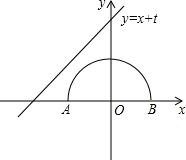 如图,半圆的圆心与坐标原点重合,圆的半径为1,直线l的解析式为y=x+t.若直线l与半圆只有一个交点,则t的取值范围是________;若直线l与半圆有交点,则t的取值范围是________.
如图,半圆的圆心与坐标原点重合,圆的半径为1,直线l的解析式为y=x+t.若直线l与半圆只有一个交点,则t的取值范围是________;若直线l与半圆有交点,则t的取值范围是________.