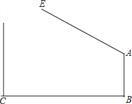
ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΒψOΈΣΉχ±ξ‘≠ΒψΘ§ΒψA‘Ύx÷αΒΡΗΚΑκ÷α…œΘ§÷±œΏy=©¹![]() x+
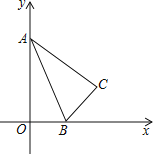
x+![]() ”κx÷αΓΔy÷αΖ÷±πΫΜ”ΎBΓΔCΝΫΒψΘ§ΥΡ±Ώ–ΈABCDΈΣΝβ–ΈΘ°
”κx÷αΓΔy÷αΖ÷±πΫΜ”ΎBΓΔCΝΫΒψΘ§ΥΡ±Ώ–ΈABCDΈΣΝβ–ΈΘ°
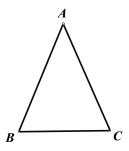
Θ®1Θ©»γΆΦ1Θ§«σΒψAΒΡΉχ±ξΘΜ
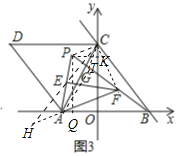
Θ®2Θ©»γΆΦ2Θ§Ν§Ϋ”ACΘ§ΒψPΈΣΓςACDΡΎ“ΜΒψΘ§Ν§Ϋ”APΓΔBPΘ§BP”κACΫΜ”ΎΒψGΘ§«“ΓœAPB=60ΓψΘ§ΒψE‘ΎœΏΕΈAP…œΘ§ΒψF‘ΎœΏΕΈBP…œΘ§«“BF=AEΘ§Ν§Ϋ”AFΓΔEFΘ§»τΓœAFE=30ΓψΘ§«σAF2+EF2ΒΡ÷ΒΘΜ
Θ®3Θ©»γΆΦ3Θ§‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§Β±PE=AE ±Θ§«σΒψPΒΡΉχ±ξΘ°
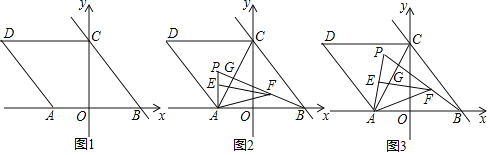
ΓΨ¥πΑΗΓΩΘ®1Θ©AΘ®©¹![]() Θ§0Θ©Θ°Θ®2Θ©49ΘΜΘ®3Θ©PΘ®©¹
Θ§0Θ©Θ°Θ®2Θ©49ΘΜΘ®3Θ©PΘ®©¹![]() Θ§3
Θ§3![]() Θ©
Θ©
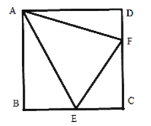
ΓΨΫβΈωΓΩΘ®1Θ©άϊ”ΟΙ¥Ι…Ε®άμ«σ≥ωBCΒΡ≥ΛΦ¥Ω…ΫβΨωΈ ΧβΘΜ
Θ®2Θ©»γΆΦ2÷–Θ§Ν§Ϋ”CEΓΔCFΘ°÷ΛΟςΓςCEF «Β»±Ώ»ΐΫ«–ΈΘ§AFΓΆCFΦ¥Ω…ΫβΨωΈ ΧβΘΜ
Θ®3Θ©»γΆΦ3÷–Θ§―”≥ΛCEΫΜFAΒΡ―”≥ΛœΏ”ΎHΘ§ΉςPQΓΆAB”ΎQΘ§PKΓΆOC”ΎKΘ§‘ΎBP…ηΫΊ»ΓBT=PAΘ§Ν§Ϋ”ATΓΔCTΓΔCFΓΔPCΘ°÷ΛΟςΓςAPF «Β»±Ώ»ΐΫ«–ΈΘ§ATΓΆPBΦ¥Ω…ΫβΨωΈ ΧβΘΜ
Θ®1Θ©»γΆΦ1÷–Θ§
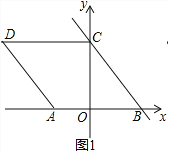
ΓΏy=-©¹![]() x+
x+![]() Θ§
Θ§
ΓύBΘ®![]() Θ§0Θ©Θ§CΘ®0Θ§
Θ§0Θ©Θ§CΘ®0Θ§![]() Θ©Θ§
Θ©Θ§
ΓύBO=![]() Θ§OC=
Θ§OC=![]() Θ§
Θ§
‘ΎRtΓςOBC÷–Θ§BC=![]() =7Θ§
=7Θ§
ΓΏΥΡ±Ώ–ΈABCD «Νβ–ΈΘ§
ΓύAB=BC=7Θ§
ΓύOA=AB-OB=7-![]() =
=![]() Θ§
Θ§
ΓύAΘ®-![]() Θ§0Θ©Θ°
Θ§0Θ©Θ°
Θ®2Θ©»γΆΦ2÷–Θ§Ν§Ϋ”CEΓΔCFΘ°
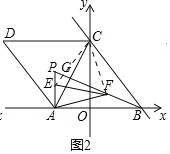
ÿOA=OBȧCOâABȧ
ΓύAC=BC=7Θ§
ΓύAB=BC=ACΘ§
ΓύΓςABC «Β»±Ώ»ΐΫ«–ΈΘ§
ΓύΓœACB=60ΓψΘ§
ΓΏΓœAPB=60ΓψΘ§
ΓύΓœAPB=ΓœACBΘ§
ΓΏΓœPAG+ΓœAPB=ΓœAGB=ΓœCBG+ΓœACBΘ§
ΓύΓœPAG=ΓœCBGΘ§ΓΏAE=BFΘ§
ΓύΓςACEΓ’ΓςBCFΘ§
ΓύCE=CFΘ§ΓœACE=ΓœBCFΘ§
ΓύΓœECF=ΓœACF+ΓœACE=ΓœACF+ΓœBCF=ΓœACB=60ΓψΘ§
ΓύΓςCEF «Β»±Ώ»ΐΫ«–ΈΘ§
ΓύΓœCFE=60ΓψΘ§EF=FCΘ§
ΓΏΓœAFE=30ΓψΘ§
ΓύΓœAFC=ΓœAFE+ΓœCFE=90ΓψΘ§
‘ΎRtΓςACF÷–Θ§AF2+CF2=AC2=49Θ§
ΓύAF2+EF2=49Θ°
Θ®3Θ©»γΆΦ3÷–Θ§―”≥ΛCEΫΜFAΒΡ―”≥ΛœΏ”ΎHΘ§ΉςPQΓΆAB”ΎQΘ§PKΓΆOC”ΎKΘ§‘ΎBP…ηΫΊ»ΓBT=PAΘ§Ν§Ϋ”ATΓΔCTΓΔCFΓΔPCΘ°
ΓΏΓςCEF «Β»±Ώ»ΐΫ«–ΈΘ§
ΓύΓœCEF=60ΓψΘ§EC=CFΘ§
ΓΏΓœAFE=30ΓψΘ§ΓœCEF=ΓœH+ΓœEFHΘ§
ΓύΓœH=ΓœCEF-ΓœEFH=30ΓψΘ§
ΓύΓœH=ΓœEFHΘ§
ΓύEH=EFΘ§
ΓύEC=EHΘ§
ΓΏPE=AEΘ§ΓœPEC=ΓœAEHΘ§
ΓύΓςCPEΓ’ΓςHAEΘ§
ΓύΓœPCE=ΓœHΘ§
ΓύPCΓΈFHΘ§
ΓΏΓœCAP=ΓœCBTΘ§AC=BCΘ§
ΓύΓςACPΓ’ΓςBCTΘ§
ΓύCP=CTΘ§ΓœACP=ΓœBCTΘ§
ΓύΓœPCT=ΓœACB=60ΓψΘ§
ΓύΓςCPT «Β»±Ώ»ΐΫ«–ΈΘ§
ΓύCT=PTΘ§ΓœCPT=ΓœCTP=60ΓψΘ§
ÿCPøFHȧ
ΓύΓœHFP=ΓœCPT=60ΓψΘ§
ΓΏΓœAPB=60ΓψΘ§
ΓύΓςAPF «Β»±Ώ»ΐΫ«–ΈΘ§
ΓύΓœCFP=ΓœAFC-ΓœΓœAFP=30ΓψΘ§
ΓύΓœTCF=ΓœCTP-ΓœTFC=30ΓψΘ§
ΓύΓœTCF=ΓœTFCΘ§
ΓύTF=TC=TPΘ§
ΓύATΓΆPFΘ§…η BF=mΘ§‘ρAE=PE=mΘ§
ΓύPF=AP=2mΘ§TF=TP=mΘ§TB=2mΘ§BP=3mΘ§
‘ΎRtΓςAPT÷–Θ§AT=![]() mΘ§
mȧ
‘ΎRtΓςABT÷–Θ§ΓΏAT2+TB2=AB2Θ§
ΓύΘ®![]() mΘ©2+Θ®2mΘ©2=72Θ§
mΘ©2+Θ®2mΘ©2=72Θ§
ΫβΒΟm=![]() Μρ-
Μρ-![]() Θ®…αΤζΘ©Θ§
Θ®…αΤζΘ©Θ§
ΓύBF=![]() Θ§AT=
Θ§AT=![]() Θ§BP=3
Θ§BP=3![]() Θ§sinΓœABT=
Θ§sinΓœABT=![]() Θ§
Θ§
ΓΏOK=PQ=BPsinΓœPBQ=3![]() ΓΝ
ΓΝ![]() =3
=3![]() Θ§BQ=
Θ§BQ=![]() =6Θ§
=6Θ§
ΓύOQ=BQ-BO=6-![]() =
=![]() Θ§
Θ§
ΓύPΘ®-![]() Θ§3
Θ§3![]() Θ©
Θ©