题目内容
【题目】如图，图1为边长为a的大正方形中有一个边长为b的小正方形，图2是由图1中阴影部分拼成的一个长方形．
（1）设图1中阴影部分面积为S1，图2中阴影部分面积为S2，请用含a、b的代数式表示：S1= ， S2=（只需表示，不必化简）；
（2）以上结果可以验证哪个乘法公式？请写出这个乘法公式；
（3）运动（2）中得到的公式，计算：20152﹣2016×2014．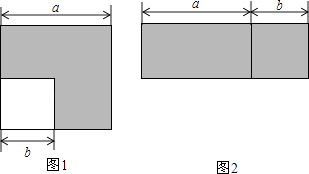 
【答案】
（1）a2﹣b2；（a+b）（a﹣b）
（2）（a+b）（a﹣b）=a2﹣b2
（3）解：20152﹣2016×2014
=20152﹣（2015+1）（2015﹣1）
=20152﹣（20152﹣1）
=20152﹣20152+1
=1
【解析】解：（1）大正方形的面积为a2 ， 小正方形的面积为b2 ， 故图1阴影部分的面积值为a2﹣b2；
长方形的长和宽分别为（a+b）、（a﹣b），
故图2重拼的长方形的面积为（a+b）（a﹣b）；
2）比较上面的结果，都表示同一阴影的面积，它们相等，
即（a+b）（a﹣b）=a2﹣b2 ， 可以验证平方差公式，这也是平方差公式的几何意义；
所以答案是：（a+b）（a﹣b）=a2﹣b2；
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
