Question

抛物线y=x²上有三点A、B、C，其横坐标分别是m、m+1、m+3，请你探究△ABC的面积S是否为定值，若是，请求出这个值；若不是，请你求出S与m的函数关系式．

Answer 1

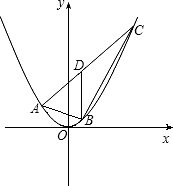解：S是定值；
A（m，m²），B（m+1，（m+1）²），C（m+3，（m+3）²），
设直线AC的解析式为y=kx+b，则有

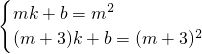
解得：k=2m+3b=-m²-3m，y=（2m+3）x-m²-3m，
BD的长为（2m+3）（m+1）-m²-3m-（m+1）²=2，
．
分析：把横坐标代入抛物线解析式，可得相应的纵坐标；设出直线AC的解析式，把A，C两点代入，即可求得直线AC的解析式，作BD∥y轴，交直线AC于点D，可得BD的长度，那么△ABC的面积可分为△ADB和△CDB的和，把相关数值代入即可求解．
点评：用到的知识点为：抛物线中三角形的面积分为一边平行于坐标轴的两个三角形的面积的和计算比较简便．