Question

抛物线y=x²上有三点P₁、P₂、P₃，其横坐标分别为t，t+1，t+3，则△P₁P₂P₃的面积为（　　）

• A、1
• B、2
• C、3
• D、4

Answer 1

分析：分别从点P₁、P₂、P₃向x轴作垂线构造梯形，利用面积差求解．则△P₁P₂P₃的面积为：

1

2

×3[t²+（t+3）²]-

1

2

[（t+1）²+t²]-

1

2

×2[（t+1）²+t²]=3．

解答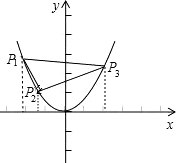：解：分别从点P₁、P₂、P₃向x轴作垂线，因为P₁、P₂、P₃，
其横坐标分别为t，t+1，t+3，而三点在抛物线y=x²上，
所以三点纵坐标分别是：t²，（t+1）²，（t+3）²，
则S_△P1P2P3=

1

2

×3×[t²+（t+3）²]-

1

2

×[（t+1）²+t²）]-

1

2

×2×[（t+1）²+（t+3）²]=3．
故选C．

点评：主要考查了梯形的面积公式的运用和一次函数图象上点的坐标特征，要会根据点的坐标求出所需要的线段的长度，灵活运用勾股定理和面积公式求解．