题目内容
【题目】如图,⊙O的直径AB=12cm,C为AB延长线上一点,CP与⊙O相切于点P,过点B作弦BD∥CP,连接PD.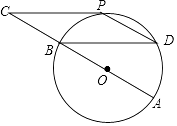
(1)求证:点P为 ![]() 的中点;
的中点;
(2)若∠C=∠D,求四边形BCPD的面积.
【答案】
(1)证明:连接OP, 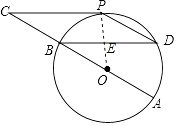
∵CP与⊙O相切于点P,
∴PC⊥OP,
∴∠OPC=90度,
∵BD∥CP,
∴∠OEP=OPC=90度,
∴BD⊥OP,
∴点P为 ![]() 的中点.
的中点.
(2)解:∵∠C=∠D,
∵∠POB=2∠D,
∴∠POB=2∠C,
∵∠CPO=90°,
∴∠C=30°,
∵BD∥CP,
∴∠C=∠DBA,
∴∠D=∠DBA,
∴BC∥PD,
∴四边形BCPD是平行四边形,
∵PO= ![]() AB=6,
AB=6,
∴PC=6 ![]() ,
,
∵∠ABD=∠C=30°,
∴OE= ![]() OB=3,
OB=3,
∴PE=3,
∴四边形BCPD的面积=PCPE=6 ![]() ×3=18
×3=18 ![]() .
.
【解析】(1)由切线性质定理和垂径定理推论可证出;(2)由圆周角定理可得出∠POB=2∠C,∠CPO=90°,∠C=30°,求出底边长和高,即能求出其面积.
【考点精析】利用平行四边形的判定与性质和垂径定理对题目进行判断即可得到答案,需要熟知若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.

【题目】科技馆门票价格规定如下表:
购票张数 |
|
| 100张以上 |
每张票的价格 | 18元 | 15元 | 10元 |
风鸣学校七年级![]() 、
、![]() 两个科技班共103人去科技馆,其中
两个科技班共103人去科技馆,其中![]() 班有40多人不足50人
班有40多人不足50人![]() 经计算,如果两个班都以班为单位购票,则一共应付1686元.
经计算,如果两个班都以班为单位购票,则一共应付1686元.
![]() 如果两个班联合起来,作为一个团体购票,可以省______元
如果两个班联合起来,作为一个团体购票,可以省______元![]()
![]() 七年级
七年级![]() 班有多少学生?
班有多少学生?
![]() 如果七年级
如果七年级![]() 班单独组织去科技馆,作为组织者,你如何购票才最省钱?
班单独组织去科技馆,作为组织者,你如何购票才最省钱?
【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产![]() 、
、![]() 两种产品共50件.已知生产一件
两种产品共50件.已知生产一件![]() 种产品需用甲种原料9千克,乙种原料3千克,可获利润700元;生产一件
种产品需用甲种原料9千克,乙种原料3千克,可获利润700元;生产一件![]() 种产品需用甲种原料4千克,乙种原料10千克,可获利润1200元.
种产品需用甲种原料4千克,乙种原料10千克,可获利润1200元.
(1)设生产![]() 种产品
种产品![]() 件,完成表格:
件,完成表格:
|
| |
生产数量(件 |
| 件 |
需甲种原料(千克) |
|
|
需乙种原料(千克) |
|
|
(2)按要求安排![]() 、
、![]() 两种产品的件数有几种方案?请你设计出来.
两种产品的件数有几种方案?请你设计出来.
(3)以上方案哪种利润最大?是多少元?