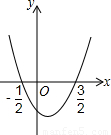��Ŀ����
��֪��ͼ��ʾ�����κ���y=3x2-3��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ߣ�����y�ύ�ڵ�C��ֱ��x=1+ m��m��O����x�ύ�ڵ�D��
m��m��O����x�ύ�ڵ�D��
��1����A��B��C��������꣮
��2����ֱ��x=l+m��m��0������һ��P����P�ڵ�һ���ޣ���ʹ����P��D��BΪ���������������B��C��OΪ��������������ƣ���P������꣨�ú�m�Ĵ���ʽ��ʾ����
��3���ڣ�2�������������£����ʣ�������y=3x2-3���Ƿ����һ��Q��ʹ���ı���ABPQΪƽ���ı��Σ�������������ĵ�Q�������m��ֵ����������ڣ����Ҫ˵�����ɣ�
 m��m��O����x�ύ�ڵ�D��
m��m��O����x�ύ�ڵ�D����1����A��B��C��������꣮
��2����ֱ��x=l+m��m��0������һ��P����P�ڵ�һ���ޣ���ʹ����P��D��BΪ���������������B��C��OΪ��������������ƣ���P������꣨�ú�m�Ĵ���ʽ��ʾ����
��3���ڣ�2�������������£����ʣ�������y=3x2-3���Ƿ����һ��Q��ʹ���ı���ABPQΪƽ���ı��Σ�������������ĵ�Q�������m��ֵ����������ڣ����Ҫ˵�����ɣ�
��������1����y=0�������x��һԪ���η��̼��ɵõ���A��B�����꣬��x=0�����y��ֵ���ɵõ���C�����ꣻ
��2�����ݵ�B��C���������OB��OC�ij��ȣ������BD�ij��ȣ�Ȼ��֢�OB��BD�Ƕ�Ӧ�ߣ���OC��BD�Ƕ�Ӧ�ߣ��������������ζ�Ӧ�߳ɱ����г�����m�ķ��̣����ɵõ���P�����ꣻ
��3������ƽ���ı��εĶԱ�ƽ���������m��ʾ����Q�����꣬�ٸ��ݵ�Q���������ϣ����������߽���ʽ�������m��ֵ�����ɵý⣮
��2�����ݵ�B��C���������OB��OC�ij��ȣ������BD�ij��ȣ�Ȼ��֢�OB��BD�Ƕ�Ӧ�ߣ���OC��BD�Ƕ�Ӧ�ߣ��������������ζ�Ӧ�߳ɱ����г�����m�ķ��̣����ɵõ���P�����ꣻ
��3������ƽ���ı��εĶԱ�ƽ���������m��ʾ����Q�����꣬�ٸ��ݵ�Q���������ϣ����������߽���ʽ�������m��ֵ�����ɵý⣮
����⣺��1����y=0����3x2-3=0��
���x1=-1��x2=1��
���ԣ���A��-1��0����B��1��0����
��x=0����y=3��0-3=-3��
���ԣ���C������Ϊ��0��-3����
��2����B��1��0����C��0��-3����
��OB=1��OC=3��
�֡�ֱ��x=l+m��m��O����x�ύ�ڵ�D��
��BD=1+m-1=m��
��OB��BD�Ƕ�Ӧ��ʱ��
�ߡ�BCO�ס�BPD��
��
=
��
��
=
��
���PD=3m��
���ԣ���ʱ��P�������ǣ�1+m��3m����
��OC��BD�Ƕ�Ӧ��ʱ��
�ߡ�BCO�ס�PBD��
��
=
��
��
=
��
���PD=
m��
���ԣ���ʱ��P������Ϊ��1+m��
m����
��3�����ڣ��������£�
��A��-1��0����B��1��0����
��AB=1-��-1��=1+1=2��
����ƽ���ı��εĶԱ�ƽ������ȣ�PQ=AB=2����PQ��AB��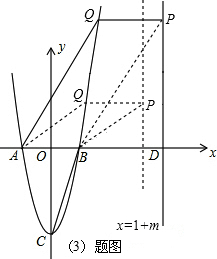
�ٵ���P��1+m��3m��ʱ��1+m-2=m-1��
���ԣ���Q������Ϊ��m-1��3m����
�ߵ�Q���������ϣ�
��3��m-1��2-3=3m��
�����ã�m2-3m=0��
��ã�m1=3��m2=0����ȥ����
�ڵ���P��1+m��
m��ʱ��1+m-2=m-1��
���ԣ���Q������Ϊ��m-1��
m����
�ߵ�Q���������ϣ�
��3��m-1��2-3=
m��
�����ã�9m2-19m=0��
���m1=
��m2=0����ȥ����
��3��
������0��
��������y=3x2-3�ϴ��ڵ�Q��ʹ���ı���ABPQΪƽ���ı��Σ�
��ʱ��m��ֵΪ3��
��
���x1=-1��x2=1��
���ԣ���A��-1��0����B��1��0����
��x=0����y=3��0-3=-3��

���ԣ���C������Ϊ��0��-3����
��2����B��1��0����C��0��-3����
��OB=1��OC=3��
�֡�ֱ��x=l+m��m��O����x�ύ�ڵ�D��
��BD=1+m-1=m��
��OB��BD�Ƕ�Ӧ��ʱ��
�ߡ�BCO�ס�BPD��
��
| OB |
| BD |
| OC |
| PD |
��
| 1 |
| m |
| 3 |
| PD |
���PD=3m��
���ԣ���ʱ��P�������ǣ�1+m��3m����
��OC��BD�Ƕ�Ӧ��ʱ��
�ߡ�BCO�ס�PBD��
��
| OC |
| BD |
| OB |
| PD |
��
| 3 |
| m |
| 1 |
| PD |
���PD=
| 1 |
| 3 |
���ԣ���ʱ��P������Ϊ��1+m��
| 1 |
| 3 |
��3�����ڣ��������£�
��A��-1��0����B��1��0����
��AB=1-��-1��=1+1=2��
����ƽ���ı��εĶԱ�ƽ������ȣ�PQ=AB=2����PQ��AB��

�ٵ���P��1+m��3m��ʱ��1+m-2=m-1��
���ԣ���Q������Ϊ��m-1��3m����
�ߵ�Q���������ϣ�
��3��m-1��2-3=3m��
�����ã�m2-3m=0��
��ã�m1=3��m2=0����ȥ����
�ڵ���P��1+m��
| 1 |
| 3 |
���ԣ���Q������Ϊ��m-1��
| 1 |
| 3 |
�ߵ�Q���������ϣ�
��3��m-1��2-3=
| 1 |
| 3 |
�����ã�9m2-19m=0��
���m1=
| 19 |
| 9 |
��3��
| 19 |
| 9 |
��������y=3x2-3�ϴ��ڵ�Q��ʹ���ı���ABPQΪƽ���ı��Σ�
��ʱ��m��ֵΪ3��
| 19 |
| 9 |
�����������ۺϿ����˶��κ�������Ҫ�����˶��κ�����������Ľ������⣬���������ζ�Ӧ�߳ɱ��������ʣ�ƽ���ı��εĶԱ�ƽ������ȣ���2����Ҫע����ݶ�Ӧ�ߵIJ�ͬ��������ۣ���3������ƽ���ı��ε�������m��ʾ����Q�������ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
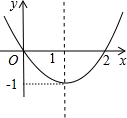 ��֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ������ֵΪ3ʱ���Ա���x��ֵΪ��������
��֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ������ֵΪ3ʱ���Ա���x��ֵΪ��������| A��3 | B��4 | C��-1 | D��-1��3 |
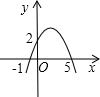 ��֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ�������н��ۣ���a��bͬ�ţ��ڵ�x=-1��x=5ʱ������ֵy��ȣ���4a+b=0���ܵ�y=2ʱ��x��ֵֻ��ȡ0��������ȷ���У�������
��֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ�������н��ۣ���a��bͬ�ţ��ڵ�x=-1��x=5ʱ������ֵy��ȣ���4a+b=0���ܵ�y=2ʱ��x��ֵֻ��ȡ0��������ȷ���У�������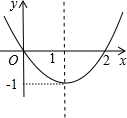 ��֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ������ֵΪ3ʱ���Ա���x��ֵΪ
��֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ������ֵΪ3ʱ���Ա���x��ֵΪ ��֪���κ���y=4x2-4x-3��ͼ����ͼ��ʾ��
��֪���κ���y=4x2-4x-3��ͼ����ͼ��ʾ��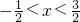 ������ֵy________0��
������ֵy________0��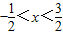 ������ֵy 0��
������ֵy 0��