题目内容
如图，在□ABCD中，点E、F是对角线AC上两点，且AE=CF．求证：∠EBF=∠FDE．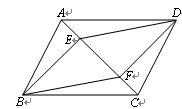
证明：在平行四边形ABCD中，则AD=BC，∠DAE=∠BCF，
又AE=CF，
∴△ADE≌△CBF，
∴DE=BF，
同理BE=DF，
∴四边形EBFD是平行四边形，
∴∠EBF=∠FDE．
又AE=CF，
∴△ADE≌△CBF，
∴DE=BF，
同理BE=DF，
∴四边形EBFD是平行四边形，
∴∠EBF=∠FDE．
通过三角形全等得出DE=BF与BE=DF，即四边形EBFD是平行四边形，即可得出结论．
练习册系列答案
阅读快车系列答案
相关题目
自B→A→E→B停止，点Q自D→F→C→D停止，点P运动的路程是m，点Q运动的路程是n，当四边形BPDQ是平行四边形时，求m与n满足的数量关系．(画出示意图)
