题目内容
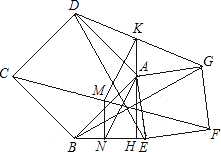 如图,两个正方形ABCD和AEFG共顶点A,连BE,DG,CF,AE,BG,K,M分别为DG和CF的中点,KA的延长线交BE于H,MN⊥BE于N.则下列结论:①BG=DE且BG⊥DE;②△ADG和△ABE的面积相等;③BN=EN,④四边形AKMN为平行四边形.其中正确的是
如图,两个正方形ABCD和AEFG共顶点A,连BE,DG,CF,AE,BG,K,M分别为DG和CF的中点,KA的延长线交BE于H,MN⊥BE于N.则下列结论:①BG=DE且BG⊥DE;②△ADG和△ABE的面积相等;③BN=EN,④四边形AKMN为平行四边形.其中正确的是
- A.③④
- B.①②③
- C.①②④
- D.①②③④
D
分析:充分利用三角形的全等,正方形的性质,平行四边形的性质依次判断所给选项的正误即可.
解答: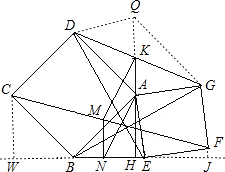 解:由两个正方形的性质易证△AED≌△AGB,
解:由两个正方形的性质易证△AED≌△AGB,
∴BG=DE,∠ADE=∠ABG,
∴可得BG与DE相交的角为90°,
∴BG⊥DE.①正确;
如图,延长AK,使AK=KQ,连接DQ、QG,
∴四边形ADQG是平行四边形;
作CW⊥BE于点W,FJ⊥BE于点J,
∴四边形CWJF是直角梯形;
∵AB=DA,AE=DQ,∠BAE=∠ADQ,
∴△ABE≌△DAQ,
∴∠ABE=∠DAQ,
∴∠ABE+∠BAH=∠DAQ+∠BAH=90°.
∴△ABH是直角三角形.
易证:△CWB≌△BHA,△EJF≌△AHE;
∴WB=AH,AH=EJ,
∴WB=EJ,
又WN=NJ,
∴WN-WB=NJ-EJ,
∴BN=NE,③正确;
∵MN是梯形WGFC的中位线,WB=BE=BH+HE,
∴MN= (CW+FJ)=
(CW+FJ)= WC=
WC= (BH+HE)=
(BH+HE)= BE;
BE;
易证:△ABE≌△DAQ(SAS),∴AK= AQ=
AQ= BE,
BE,
∴MN∥AK且MN=AK;
四边形AKMN为平行四边形,④正确.
S△ABE=S△ADQ=S△ADG= S?ADQG,②正确.
S?ADQG,②正确.
所以,①②③④都正确;
故选D.
点评:当出现两个正方形时,一般应出现全等三角形.图形较复杂,选项较多时,应用排除法求解.
分析:充分利用三角形的全等,正方形的性质,平行四边形的性质依次判断所给选项的正误即可.
解答:
 解:由两个正方形的性质易证△AED≌△AGB,
解:由两个正方形的性质易证△AED≌△AGB,∴BG=DE,∠ADE=∠ABG,
∴可得BG与DE相交的角为90°,
∴BG⊥DE.①正确;
如图,延长AK,使AK=KQ,连接DQ、QG,
∴四边形ADQG是平行四边形;
作CW⊥BE于点W,FJ⊥BE于点J,
∴四边形CWJF是直角梯形;
∵AB=DA,AE=DQ,∠BAE=∠ADQ,
∴△ABE≌△DAQ,
∴∠ABE=∠DAQ,
∴∠ABE+∠BAH=∠DAQ+∠BAH=90°.
∴△ABH是直角三角形.
易证:△CWB≌△BHA,△EJF≌△AHE;
∴WB=AH,AH=EJ,
∴WB=EJ,
又WN=NJ,
∴WN-WB=NJ-EJ,
∴BN=NE,③正确;
∵MN是梯形WGFC的中位线,WB=BE=BH+HE,
∴MN=
 (CW+FJ)=
(CW+FJ)= WC=
WC= (BH+HE)=
(BH+HE)= BE;
BE;易证:△ABE≌△DAQ(SAS),∴AK=
 AQ=
AQ= BE,
BE,∴MN∥AK且MN=AK;
四边形AKMN为平行四边形,④正确.
S△ABE=S△ADQ=S△ADG=
 S?ADQG,②正确.
S?ADQG,②正确.所以,①②③④都正确;
故选D.
点评:当出现两个正方形时,一般应出现全等三角形.图形较复杂,选项较多时,应用排除法求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
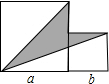 如图,两个正方形边长分别为a、b,
如图,两个正方形边长分别为a、b,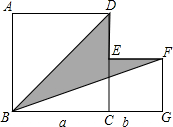 如图,两个正方形的边长分别为a和b,如果a+b=10,ab=20,那么:
如图,两个正方形的边长分别为a和b,如果a+b=10,ab=20,那么: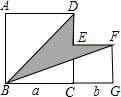 如图,两个正方形边长分别为a、b,如果a+b=17,ab=60,求阴影部分的面积.
如图,两个正方形边长分别为a、b,如果a+b=17,ab=60,求阴影部分的面积. 如图,两个正方形边长分别为a、b,
如图,两个正方形边长分别为a、b,